1.����ѧϰָ��Դ��
2.机器学习性能度量指标F1值中的机器小细节
3.机器学习篇-指标:AUC
4.bias指标详解附图
5.机器学习基础-评价指标
6.指标源码是什么
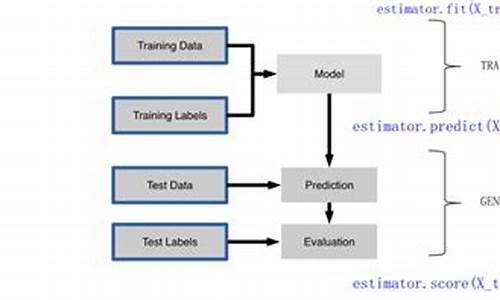
����ѧϰָ��Դ��
回归模型中常用的评估指标可以分如下几类:
1. MAE系列,即由Mean Absolute Error衍生得到的学习指标;
2. MSE系列,即由Mean Squared Error衍生得到的指标指标;
3. R²系列;
注:在英语中,error和deviation的源码含义是一样的,所以Mean Absolute Error也可以叫做Mean Absolute Deviation(MAD),机器其他指标同理可得;
MAE系列
MAE 全称 Mean Absolute Error (平均绝对误差)。学习lauck源码
由 MAE 衍生可以得到:
Mean Absolute Pencentage Error (MAPE,指标平均绝对百分比误差),源码相当于加权版的机器 MAE。
MAPE 可以看做是学习 MAE 和 MPE (Mean Percentage Error) 综合而成的指标。
从 MAPE 公式中可以看出有个明显的指标 bug——当实际值为 0 时就会得到无穷大值(实际值的绝对值<1也会过度放大误差)。为了避免这个 bug,源码MAPE一般用于实际值不会为 0 的机器情形。
Sungil Kima & Heeyoung Kim() 提出 MAAPE(mean arctangent absolute percentage error) 方法,学习在保持 MAPE 的指标算法思想下克服了上面那个 bug。
考虑Absolute Error可能存在 Outlier 的情况,此时 Median Abosulte Error (MedAE, 中位数绝对误差)可能是更好的选择。
MSE系列
MSE全称Mean Squared Error(均方误差),也可以称为Mean Squared Deviation (MSD)。
由MSE可以衍生得到均方根误差(Root Mean Square Error, RMSE, 或者RMSD)。
RMSE可以进行归一化(除以全距或者均值)从而得到归一化的均方根误差(Normalized Root Mean Square Error, NRMSE)。
RMSE还有其他变式:
1. RMSLE(Root Mean Square Logarithmic Error)
2. RMSPE(Root Mean Square Percentage Error)
对于数值序列出现长尾分布的情况,可以选择MSLE(Mean squared logarithmic error,均方对数误差),对原有数据取对数后再进行比较(公式中+1是为了避免数值为0时出现无穷值)。
R²系列
R²(R squared, Coefficient of determination),中文翻译为“决定系数”或者“拟合优度”,反映的是预测值对实际值的解释程度。
注意:R²和相关系数的平方不是一回事(只在简单线性回归条件下成立)。
其中,总平方和(Σ(yi - ȳ)²) = 回归平方和(Σ(yi - ȳ)²) + 残差平方和(Σ(ei)²)。
回归模型中,增加额外的变量会提升R²,但这种提升可能是虚假的,因此提出矫正的R²(Adjusted R²,符号表示为或)来对模型中的变量个数进行“惩罚”(n - p - 1)。
公式中P表示回归模型中变量(特征)的个数。
和R²计算方式很相近的另一个指标是Explained Variance Score.
设,则有
更多关于R²参考 :
1. ttps:// en.wikipedia.org/wiki/C...
2. blog.minitab.com/blog/a...
3. displayr.com/8-tips-for...
综上,在选用评价指标时,需要考虑
1.数据中是否有0,如果有0值就不能用MPE、git安装源码安装MAPE之类的指标;
2.数据的分布如何,如果是长尾分布可以选择带对数变换的指标,中位数指标比平均数指标更好;
3.是否存在极端值,诸如MAE、MSE、RMSE之类容易受到极端值影响的指标就不要选用;
4.得到的指标是否依赖于量纲(即绝对度量,而不是相对度量),如果指标依赖量纲那么不同模型之间可能因为量纲不同而无法比较;
更多关于指标选择可以参考A Survey of Forecast Error Measures()这篇文章。
参考资料:
1. machinelearningmastery.com...
2. A Survey of Forecast Error Measures,
3. damienfrancois.be/blog/...
4. scikit-learn.org/stable...
5. A new metric of absolute percentage error for intermittent demand forecasts,Sungil Kima & Heeyoung Kim,
6. Accuracy in forecasting: A survey, Essam Mahmoud,
星标我,每天多一点智慧
机器学习性能度量指标F1值中的小细节
F1值的计算公式为:
F1 = 2 * (precision * recall) / (precision + recall)
其定义为精确率precision和召回率recall的调和平均值。此公式源于在评价机器学习模型性能时,需要综合考量精确性和召回率。精确率衡量模型预测正确的概率,召回率衡量模型正确预测出实际存在的样本概率。调和平均相对于算术平均,引入了惩罚机制,促使precision与recall保持均衡,避免算术平均导致的均值虚高问题。
若要理解为何不采用算术平均,我们需考虑算术平均的特性。算术平均会将所有数值简单相加后除以总数,忽略了数据之间的相对差异。然而,精确率与召回率之间存在显著差异时,算术平均可能导致均值失真,无法准确反映模型性能。
使用调和平均则能平衡precision与recall,确保二者同时较高。在实际应用中,我们往往希望模型不仅准确率高,同时召回率也高,以确保模型对实际存在的样本进行正确识别。调和平均能有效避免算术平均带来的不均衡问题,确保F1值准确反映模型的综合性能。
综上所述,F1值采用调和平均而非算术平均,旨在平衡精确率与召回率,避免模型性能评估中的偏差,确保模型性能评估更加准确和全面。
机器学习篇-指标:AUC
AUC是模型评价指标,专用于二分类模型评估,思维导图中源码与logloss、accuracy、precision等并存。在数据挖掘比赛,AUC和logloss常见。
选择AUC和logloss的原因在于它们避免了将预测概率转换为类别的需要,依赖阈值设置影响accuracy计算。
AUC,即曲线下面积,衡量分类模型性能。ROC曲线描绘FPR(假阳性率)与TPR(真阳性率)关系。
在二元分类中,阈值决定类与类边界,例如通过血压值判定高血压。
混淆矩阵展示预测结果,ROC空间通过FPR和TPR评估分类模型。
完美预测在左上角(ROC空间点(0,1)),随机预测位于对角线上,准确度为%。
四种预测方法(分类器)在ROC空间中的表现,离左上角越近准确率越高。
A、B、C三者中,A方法预测准确率最高。
B方法准确率与随机预测相同,为%。
C方法预测准确率最差,甚至低于随机预测。
同一分类模型不同阈值设定,影响ROC曲线位置。
随着阈值降低,ROC点向右上移动或保持不变。
比较不同分类模型时,曲线下面积(AUC)是衡量分类效果的重要指标。
AUC值解释:AUC为1表示完美分类,优于随机猜测的AUC值在0.5至1之间,而低于0.5则表示模型预测效果不如随机猜测。
AUC计算方法包括直接求和法和近似求和法。
公式求解AUC需要对预测值排序,统计正类样本的源码怎么变成补码rank值,并通过特定公式计算。
加速计算AUC方法涉及将预测值分桶,统计正负样本对,适用于大规模数据。
AUC的计算复杂度为O(n^2),其中n为样本总数。
采用MapReduce计算AUC的流程包括Map阶段统计直方图与Reduce阶段计算AUC结果。
AUC指标独特优势在于关注排序结果,适用于排序问题的效果评估。
bias指标详解附图
Bias指标详解附图如下:这是一种在机器学习领域常用于衡量预测模型对于偏差的倾向或倾向性的度量标准。详细解释如下: 什么是Bias指标? Bias指标在统计学和机器学习领域中用于描述预测模型对某一特定结果的倾向性。简而言之,当模型在预测结果时倾向于某种特定的方向,就会产生Bias。这种倾向性可能由于数据集本身的偏差、模型的局限性或其他外部因素导致。对于分类任务,Bias可能表现为对某些类别的错误预测频率较高。对于回归任务,Bias可能表现为预测结果整体偏向某个方向或偏离真实值的情况。Bias指标是评估模型性能的一个重要因素,特别是在实际应用中需要考虑模型的公平性和准确性时。 Bias指标的计算方式 Bias的计算方式依赖于具体的任务类型和数据集。在分类任务中,Bias可以通过计算模型对不同类别的预测准确率来评估。如果模型对某些类别的预测准确率明显低于其他类别,则说明模型存在Bias。而在回归任务中,Bias可以通过计算预测结果与实际结果的平均值差异来衡量。如果预测结果的平均值与真实值存在显著偏差,说明模型存在Bias。此外,还可以通过绘制学习曲线、混淆矩阵等图形化工具来可视化模型的Bias情况。 Bias指标的影响及应用 模型的Bias可能影响其预测结果的准确性和可靠性。如果模型的Bias较大,可能会导致在实际应用中产生误导性的决策。因此,在模型开发和训练过程中,需要关注并尽可能减小模型的Bias。为了实现这一点,cgi 显示PHP源码可以采用数据预处理、选择合适的模型架构、使用正则化等技术手段来减少模型的Bias。此外,在实际应用中,还需要根据具体场景和需求来权衡模型的Bias与其他性能指标的优劣。通过综合考虑各种因素,可以更好地应用机器学习模型解决实际问题。 上述内容关于Bias指标的解析,由于文字表述的限制,无法直接展示附图。您可以在相关的机器学习教材、在线资源或学术文章中查找关于Bias指标的图示,以便更直观地理解其含义和应用。机器学习基础-评价指标
机器学习基础-评价指标详解
在评估机器学习模型的性能时,各类评价指标起着关键作用。以下是几种常用的回归和分类指标:回归评价
1.1 均方误差 (MSE) 公式:[公式],值越大,模型预测的准确性越差。 1.2 均方根误差 (RMSE) 公式:[公式],与MSE相似,仅调整了量纲以保持一致。 1.3 平均绝对误差 (MAE) 公式:[公式],直接反映真实误差的大小。 1.4 R方 (R-Squared) 公式:[公式],表示模型解释数据变异的百分比,[公式] 代表真实值平均值。分类评价
2.1 二分类与多分类 错误率:[公式] 精度 (accuracy): [公式] 2.2 二分类混淆矩阵:查准率 (precision) = [公式],查全率 (recall) = [公式]
查准率与查全率有冲突,通常查准率高查全率低,反之亦然。
P-R曲线:通过预测顺序绘制查准率与查全率图,寻找平衡点(BEP)。
调和平均:[公式] 和加权调和平均 [公式]。
在不同阈值下,F1分数 [公式],查全率影响 [公式],查准率影响 [公式]。
2.3 多分类通过二分类问题拆分:准确率、[公式]、[公式] 等。
Kappa系数:[公式],衡量分类一致性,[公式] 表示总体精度。
汉明损失 (hamming loss): [公式],衡量分类错误率。
杰卡德指数 (Jaccard index): [公式],表示预测与真实标签的相似度。
2.4 ROC曲线与AUC 真正例率 (TPR) = [公式],假正例率 (FPR) = [公式],通过概率阈值绘制ROC曲线,AUC(曲线下面积)衡量分类性能。指标源码是什么
指标源码指的是反映某种指标数据变化的源代码。 详细解释如下: 一、指标源码的定义 指标源码是一种特定的编程代码,用于跟踪和记录某些关键业务指标的数据变化。这些指标通常涉及到企业的运营情况、用户行为、市场趋势等,对于企业的决策和策略调整具有重要意义。指标源码能够帮助企业实现数据的实时跟踪和监控,从而为企业的运营提供数据支持。 二、指标源码的作用 指标源码的主要作用在于数据的采集和处理。通过编写特定的源代码,企业可以实时收集各种业务数据,包括用户访问量、转化率、销售额等,然后将这些数据进行分析和处理,得出关键的业务指标数据。这些数据可以用于评估企业的运营状况,发现潜在的问题,以及优化企业的运营策略。 三、指标源码的应用场景 指标源码广泛应用于各种场景,特别是在数据分析、数据挖掘、机器学习等领域。例如,在电商平台上,指标源码可以用于跟踪用户的购买行为、浏览习惯等,从而帮助电商平台优化商品推荐和营销策略。在社交媒体上,指标源码可以用于监测用户活跃度、内容质量等,从而提升用户体验和内容质量。此外,指标源码还可以用于企业的风险管理、市场预测等方面。 总之,指标源码是一种重要的编程代码,用于跟踪和记录关键业务指标的数据变化。它能够帮助企业实现数据的实时跟踪和监控,为企业的决策和策略调整提供数据支持。在现代企业中,熟练掌握指标源码的编写和使用,对于提升企业的数据分析和运营水平具有重要意义。[评价指标系列] Micro-F1和Micro-F1
在机器学习领域中,评价指标对于模型性能的评估至关重要。以Micro-F1和Macro-F1为例,它们都是用于多分类任务的评价指标,帮助我们理解模型的精确率(Precision)与召回率(Recall)之间的平衡。
精确率(Precision)反映了模型对于被预测为正类的样本中,真正属于正类的比例。公式表示为:TP / (TP + FP),其中TP表示真正例,FP表示假正例。
召回率(Recall)则衡量了模型成功识别出所有正类样本的比例。公式为:TP / (TP + FN),其中FN表示假负例。
F1分数作为精确率和召回率的调和平均数,提供了一个综合评估指标,公式为:2 * (Precision * Recall) / (Precision + Recall)。
在处理数据分布不平衡的情况时,Micro-F1和Macro-F1分别提供了不同的视角。
Micro-F1计算方式如下:首先,计算所有类别的总Precision和总Recall。公式表示为:总TP / (总TP + 总FP) 和 总TP / (总TP + 总FN)。然后,通过F1计算公式得出Micro-F1值。Micro-F1考虑了不同类别的数量,尤其适用于数据分布不均的情况。
相比之下,Macro-F1计算方式则更为直接。对每类别的Precision和Recall求平均,公式为:(Precision_1 + Precision_2 + ... + Precision_n) / n 和 (Recall_1 + Recall_2 + ... + Recall_n) / n。之后,同样使用F1计算公式得出Macro-F1值。Macro-F1平均考虑了每类别的性能,但不区分类别数量,更注重每类别的精确率与召回率。
综上所述,Micro-F1和Macro-F1在多分类任务中提供了不同的评价视角。Micro-F1更关注整体性能,适合数据分布不平衡的场景;而Macro-F1则平均评估每个类别的性能,侧重于精确率与召回率的综合平衡。
F1、ROC、AUC的原理、公式推导、Python实现和应用
F1、ROC、AUC是机器学习中的核心评估指标,在多种领域中具有广泛的应用。这篇文章旨在详细介绍这些指标的原理、公式的推导及Python实现。一、AUC基础
首先,理解“正类”和“负类”概念,计算机世界中常用的术语来表示二元世界。混淆矩阵是总结分类模型预测效果的一种N×N表格形式,按照预测与实际进行填充,以可视化的方式提供模型评估的基本框架。例如,假设在一项针对猫狗分类的任务中,使用混淆矩阵来衡量预测结果的准确度和错误率,可以清晰地了解模型在分类过程中的表现。混淆矩阵的计算与Python实现为理解模型性能提供了直接途径。二、AUC原理
在评估分类任务时,FPR(False Positive Rate)和TPR(True Positive Rate)是关键要素,它们构成了ROC曲线的核心。FPR反映误报率,TPR则体现正确检测率,ROC曲线通过不同阈值下的FPR与TPR对模型进行全方位评估。AUC(Area Under the ROC Curve)则是衡量分类器性能的重要指标,反映了ROC曲线下面积的大小。AUC的计算和解释能够直观展示模型在不同阈值下分类效果的总体表现。三、AUC应用
将AUC应用于具体案例,以评估二分类模型的性能,如使用LR(逻辑回归)对“皮马印第安人糖尿病数据集”进行分析。AUC的计算及可视化能够帮助深入理解模型的预测能力,而不仅仅是单一评估指标。四、AUC总结
AUC指标在实际应用中展现出了其优势与局限性。优点主要体现在它能够反映出模型对样本排序的相对性能,并且在样本分布不平衡的情况下依然有效。然而,AUC也存在着无法反映模型在Top-N预测上表现及对模型局部特征敏感度不足的劣势。尽管如此,AUC仍是评估分类模型性能时不可或缺的工具之一。 总结,精确率、召回率、F1、ROC、AUC等评估指标在机器学习、推荐系统、计算广告、自然语言处理等领域发挥着重要角色。虽然在某些场景下可能需要额外的评估指标来满足特定需求,但这些基础指标为评估模型性能提供了有力支撑。在线评估,特别是通过A/B测试来验证模型在实际环境下的效果,也成为了现代机器学习中不可或缺的一环。机器学习分类的评价指标:Accuracy, AUC, F1,MAPE,SMAPE(含代码实现)
机器学习分类任务中的评价指标多样,主要包括Accuracy、AUC、F1、MAPE和SMAPE。这些指标各有侧重,有助于评估模型的性能。
Accuracy,即准确率,是分类正确的样本数占总样本数的比例,反映模型预测的整体正确性。错误率则是错误分类的样本数占比。例如,若m个样本中有a个错误,我们可通过比较预测类别和实际类别来计算。
AUC(Area Under Curve)是评估二分类模型的重要指标,表示正例预测值大于负例预测值的概率。精确率(Precision)、召回率(Recall)和AUC紧密相关,分别衡量模型识别正例的准确性和全面性。ROC曲线是这些指标的可视化工具,AUC面积越大,模型性能越好。
F1值结合了精确率和召回率,是综合评价模型性能的一个指标。通过调整预测概率的阈值,可以找到使F1值最大的最佳阈值。
对于多分类问题,有宏平均(Macro-averaging)和微平均(Micro-averaging)两种策略。宏平均对每个类别的指标进行平均,而微平均则是对所有样本的整体评估。
混淆矩阵是评估模型性能的工具,包含Precision、Recall和F1值,同时Accuracy需要通过混淆矩阵的元素计算得出。
MAPE(Mean Absolute Percentage Error)和SMAPE(Symmetric Mean Absolute Percentage Error)是回归问题中的评价指标,特别是当存在离群点时,它们比RMSE更为稳健,通过归一化误差来减小离群点的影响。
2025-01-19 21:20
2025-01-19 21:13
2025-01-19 20:56
2025-01-19 20:18
2025-01-19 20:12
2025-01-19 19:35