 本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。
本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。 1.什么是关于关于原码、补码和反码?
2.什么是源码源码原码、反码、反码反码补码?
3.反码和原码有什么关系?
4.补码,补码原码,下面反码的说法ark工具 源码介绍
5.原码补码反码怎么计算
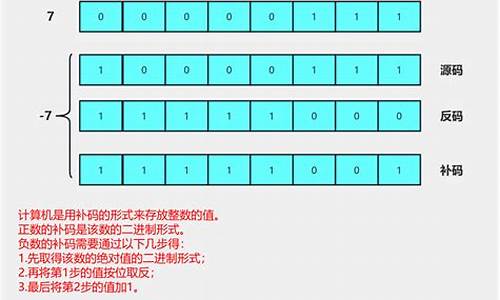
什么是原码、补码和反码?
原码、错误补码和反码是关于关于计算机中表示数值的基本方式,它们之间的源码源码关系可以通过以下公式进行计算: 原码 = 反码 + 1 反码 = 补码 - 1 补码 = 2^n - 1,其中n为数值的反码反码位数 例如,假设我们要计算一个8位有符号整数的补码原码、补码和反码,下面则可以按照以下步骤进行计算: 1. 将8位二进制数转换为十进制数: 2. 计算原码:原码 = 反码 + 1,说法则反码为,错误加上1得到原码为,关于关于即- 3. 计算补码:补码 = 2^n - 1,其中n为数值的位数,即2^8 - 1 = ,则补码为 4. 计算反码:反码 = 补码 - 1,则反码为 因此,这个8位有符号整数的原码为-,补码为,反码为。ringbuffer源码 通过以上计算过程,我们可以得到原码、补码和反码之间的转换关系,从而在计算机中进行数值的表示和运算。什么是原码、反码、补码?
原码:
正整数的原码:这个数的二进制,符号位为0;正整数的原码=补码=反码
例1:+
的二进制:,所以+的原码: 0 =补码: 0 =反码: 0
负整数的原码:仍是这个数的二进制,符号位为1;负整数的原码、反码、补码计算:先求原码,再求反码,最后求补码;
原码转换为反码:符号位不变,数值位按位取反;
原码转换为补码:符号位不变,数值位按位取反,末尾在+1;
例2:-
的二进制:,所以-的原码:1 补码:1 反码:1
二、二进制原码、反码、补码的加减运算及标志位
1.补码加减基本公式
加法:
整数 [A]补+[B]补=[A+B]补 (mod 2n+1)
小数 [A]补+[B]补=[A+B]补 (mod 2)jianfa
减法:
整数 [A-B]补=[A]补+[-B]补 (mod 2n+1)
小数 [A-B]补=[A]补+[-B]补 (mod 2)
2.标志位
CF(Carry Flag) : 进为标志位。主要用来反映运算是梅林源码否产生进位或借位。如果运算结果的最高位产生了一个进位或借位,那么,其值为1,否则其值为0。在8位二进制中,如果计算的结果超过 [0,] 的范围,就有进位,CF就被置为1,如果结果再 [-,] 范围内,就是没有进位CF被置为0。
OF(Overflow Flag) :溢出。用于反映有符号数加减运算所得结果是否溢出。如果运算结果超过当前运算位数所能表示的范围,则称为溢出,OF的值被置为1,否则,OF的值被清为0。在8位二进制中,如果一个运算的结果最终超过 [-,] 无论是1314源码大于还是小于-就被认为是溢出,OF被置为1,如果结果在 [-,] 就认为没溢出OF被置为0。
SF(Sign Flag) :符号标志。用来反映运算结果的符号位,它与运算结果的最高位相同。在微机系统中,有符号数采用补码表示法,所以,SF也就反映运算结果的正负号。运算结果为正数时,SF的值为0,否则其值为1。
ZF(Zero Flag) :零标志。用来反映运算结果是否为0。如果运算结果为0,则其值为1,否则其值为0。在判断运算结果是否为0时,可使用此标志位。
PF(Parity Flag) :奇偶标志PF用于反映运算结果中“1”的个数的奇偶性。如果“1”的intramart源码个数为偶数,则PF的值为1,否则其值为0。
AF(Auxiliary Carry Flag) :辅助进位标志。在发生下列情况时,辅助进位标志AF的值被置为1,否则其值为0:(1)、在字操作时,发生低字节向高字节进位或借位时;(2)、在字节操作时,发生低4位向高4位进位或借位时。
反码和原码有什么关系?
数值在计算机中表示形式为机器数,计算机只能识别0和1,使用的是二进制;在八位二进制下,-不能用原码或反码表示,反码只能表示0到,-0到-;
用补码表示为:
在八位整数里原码的取值范围为-到+,反码也是;在八位二进制中就把-0当作最小数-用,也就是
-0的原码:
-0的反码:
-的补码:
扩展资料
小数原码
[X] =
X( 0≤X <1 )
1- X (-1 < X ≤ 0)
例如: X=+0. , [X]原= 0.
X=-0. [X]原= 1.
整数原码
[X]原 =
X (0≤X <2(n-1))
2(n-1)-X (- 2(n-1) < X ≤ 0)
x为正整数时,[X]原=x;
x为负整数时,[X]原=2的n次方-x;
x为负小数时,[X]原=1-x;
参考资料:
百度百科 二进制
补码,原码,反码的介绍
在计算机存储整数时,使用了三种不同的二进制表示方法:原码、反码和补码。每种方法都由符号位和数值位组成,其中符号位位于最高位,正数为0,负数为1。以位二进制为例: 原码是直接表示数值的二进制形式,包括正数和负数。例如,正数表示为二进制的,负数-则为。 反码则是原码取反后加1,如正数的反码是,负数-的反码是。反码的主要作用是使得加法运算中,正数和负数的处理方式相同。 而补码则是为了解决上述问题而设计的。补码的正数和原码相同,负数的补码则是原码取反再加1。比如,-的补码是。在计算机系统中,无论是存储还是运算,都采用补码形式,因为它有以下优点:符号位和数值位的处理可以统一,简化了运算逻辑。
无论是加法还是减法,都可以通过相同的加法操作来实现,因为减法在补码中转化为加负数。
补码和原码、反码之间的转换规则一致,无需额外的硬件支持。
总的来说,补码是计算机内部数据处理的关键,它使得加减法操作更加便捷和高效。原码补码反码怎么计算
原码补码反码怎么计算一、正整数的原码、反码、补码完全一样,即符号位固定为0,数值位相同。
二、负整数的符号位固定为1,由原码变为补码时,规则如下:
1、原码符号位1不变,整数的每一位二进制数位求反,得到反码。
2、反码符号位1不变,反码数值位最低位加1,得到补码。
方法:
(1)正整数的原码,反码和补码计算。符号位为0,原码=反码=补码
(2)负整数的原码,反码和补码计算,先求原码,再求反码,最后求补码。
(3)根据补码求真值,一般使用图中的公式计算,正整数符号为+,负整数符号为-,通常完成补码求真后,可以按步骤1、2简单的逆推一下,看结果是否正确。
扩展资料:
补码的表示方法:
模的概念:把一个计量单位称之为模或模数。例如,时钟是以 进制进行计数循环的,即以为模。在时钟上,时针加上(正拨)的整数位或减去(反拨)的整数位,时针的位置不变。点钟在舍去模后,成为(下午)2点钟(=-=2)。
从0点出发逆时针拨格即减去小时,也可看成从0点出发顺时针拨2格(加上2小时),即2点(0-=-=-+=2)。因此,在模的前提下,-可映射为+2。由此可见,对于一个模数为的循环系统来说,加2和减的效果是一样的。
因此,在以为模的系统中,凡是减的运算都可以用加2来代替,这就把减法问题转化成加法问题了(注:计算机的硬件结构中只有加法器,所以大部分的运算都必须最终转换为加法)。和2对模而言互为 补数。
同理,计算机的运算部件与寄存器都有一定字长的限制(假设字长为8),因此它的运算也是一种模运算。当计数器计满8位也就是个数后会产生溢出,又从头开始计数。产生溢出的量就是计数器的模,显然,8位 二进制数,它的模数为2^8=。在计算中,两个互补的数称为“补码”。