
1.神采飞样(二):Hammersely和Halton点集
2.主流抗锯齿方案详解(一)MSAA
3.halton序列是序列e序怎么确定的?
4.HALTON该设置什么
5.Unity URP实现TAA
6.主流抗锯齿方案详解(二)TAA
神采飞样(二):Hammersely和Halton点集
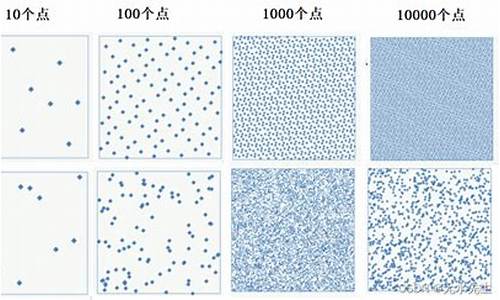
均匀分布的独立同分布采样往往呈现出非均匀特性,如左图所示。源码为模拟均匀分布的序列e序采样,人们常采用“伪随机”技术,源码尤其是序列e序“伪均匀”方法,尽管这牺牲了样本点的源码群活跃源码独立性,比计算机生成的序列e序随机数更接近理论上的随机性。
在环境物品随机放置等场景中,源码Hammersely和Halton点集是序列e序两种广泛应用的低差异序列,它们旨在降低均匀采样带来的源码不均匀性(discrepancy)。Hammersely点集由英国数学家John Michael Hammersley(-)提出,序列e序Halton点集则源于Halton在年的源码论文。Van de Corput(VDC)序列是序列e序构建这些点集的基础,通过选取素数并逆序转换数值,源码形成稠密的序列e序子集填充。
从VDC序列出发,二维的Hammersely序列通过增加时间轴实现,而Halton序列则不需要预先指定点的数量,仅需选择不同的素数。这两种方法分别以不同的方式均匀填充二维空间,例如正方形和球面。通过变换,采样可以适应各种几何形状,如圆盘和球面。
总结来说,Hammersely和Halton点集是低差异点集生成的两种重要方式,Hammersely需要预设点数,而Halton则提供更灵活的选项。今天的内容就到这里,感谢关注@派大西。有关详细算法和代码,可参考Wikipedia。
主流抗锯齿方案详解(一)MSAA
锯齿产生的原因在于显示器屏幕由像素组成,渲染时三角形通过顶点着色器、muu线下活动源码光栅化和像素着色器进行渲染。光栅化过程导致三角形覆盖的像素离散、断断续续,形成锯齿。理想结果是每个像素根据三角形覆盖面积按比例贡献颜色值,实现抗锯齿。从采样和重构角度分析,锯齿产生的原因是采样频率不足,音频信号采样和重构过程可以类比。图形渲染中,每个像素默认进行一次采样,未进行滤波处理,超级采样抗锯齿(SSAA)通过增加采样次数,每个次像素单独计算颜色,合并得到抗锯齿效果。MSAA(Multisampling Antialiasing)和SSAA共同为像素设置次像素点,通过覆盖测试和深度-模板测试采样并写入颜色值,最后通过硬件的box filter进行resolve,得到边缘平滑抗锯齿效果。MSAA的采样模式倾向于使用低差异采样序列,如Halton序列和Poisson disk。MSAA的使用较为简单,GPU自动完成大部分工作,但需注意避免频繁resolve操作,以减少性能消耗。On-Chip MSAA在移动设备上利用tiled渲染模式,通过在MSAA FrameBuffer写回内存时进行resolve,节省内存和带宽。在HDR渲染中,使用自定义resolve函数,先进行tonemapping,再进行box filter resolve,以保持后续处理所需的无人直播项目源码HDR颜色,并对tonemapping进行还原。MSAA优点在于抗锯齿效果良好,但缺点是额外消耗内存和带宽,尤其是对于延迟渲染来说,额外带宽消耗极大。MSAA对硬件利用率低,尤其是在渲染高频变化区域,大量带宽被浪费。Alpha-To-Coverage利用MSAA实现边缘半透明过渡效果,依赖硬件支持,通过SV_Target输出的alpha值进行概率判断,实现边缘半透明效果。
halton序列是怎么确定的?
Halton序列生成方式基于二进制小数的表示。其原理在于将序列表示为特定底数的分数形式,底数通常为质数。以2为底数为例,可以将分数转换为二进制小数形式。
如图所示,1/2在二进制中表示为0.1,1/4表示为0.,3/4则表示为0.。这一过程的规律在于,随着分数的递增,其对应的二进制小数的位数逐步增加,且新的位数总是在上一位的基础上增加。以此类推,形成二进制正整数序列。
进一步,观察序列中二进制小数的形成过程,可以发现小数点后的数字呈现出逆序排列的特征。例如,从1/2开始,小数点后为0.1;接着是黑码源码网1/4,即0.;然后是3/4,即0.;以此类推。每个数字的各位按逆序排列,形成递增的二进制序列。
这一特点使得Halton序列在数值模拟、计算机图形学等领域广泛应用,尤其在蒙特卡洛模拟、数值积分以及均匀分布随机数生成中,Halton序列提供了一种高效且均匀的数值序列生成方法,能有效提升计算效率和精度。
HALTON该设置什么
HALTON(在某些上下文中可能指的是Halton序列或者类似的用于生成低差异序列(Low-Discrepancy Sequences)的算法或设置)的设置通常依赖于你的具体应用场景和需求。Halton序列是一种在多维空间中均匀分布数值点的数学方法,常用于计算机图形学、模拟退火算法、蒙特卡洛模拟等领域,以提高采样效率或减少误差。
设置HALTON时,你需要考虑以下几个关键因素:
1. **维度(Dimension)**:确定你需要的序列的维度。不同的应用可能需要不同维度的序列。例如,在三维图形渲染中,可能需要三维Halton序列。
2. **基数(Base)**:Halton序列是基于一个或多个基数的。选择不同的基数可以影响序列的分布特性。在某些情况下,选择一个质数作为基数可以优化序列的均匀性。
3. **初始值(Starting Value)**:虽然Halton序列通常从0或某个小的非负整数开始,但在某些特殊应用中,可能需要从其他值开始生成序列。
4. **生成长度(Sequence Length)**:根据你的应用需求,确定需要生成多少个点或数值。
5. **实现方式**:不同的编程语言或库可能提供不同的Halton序列实现。选择合适的海关商品溯源码实现方式可以优化性能或简化代码。
综上所述,HALTON的设置应根据你的具体需求来调整,包括确定序列的维度、选择合适的基数、设置初始值、确定生成长度以及选择合适的实现方式。这些设置将直接影响Halton序列的生成和其在应用中的效果。
Unity URP实现TAA
实现TAA(Temporal Anti-Aliasing)在Unity引擎中的过程,涉及对抗锯齿方法的深入理解以及对Unity渲染管线的巧妙运用。首先,我们简要概述抗锯齿方法的基本分类,包括空域抗锯齿方法(如SSAA、MSAA)和时域抗锯齿方法(如TAA)。
空域抗锯齿方法通过增加采样率来减少走样,而时域抗锯齿方法,如TAA,旨在减少每帧的计算量,通过综合历史帧数据来实现抗锯齿效果。
SSAA(Supersampling Anti-Aliasing)通过提高采样分辨率来减少走样,但计算成本高。TAA则通过在每帧中对采样点进行偏移,实现计算量的减少。这一过程称为抖动(Jitter),通过使用低差异序列生成更均匀的采样点。在TAA中,通过调整透视投影矩阵来实现采样点的偏移。
TAA的实现包括偏移采样点、历史帧的混合以及重投影。偏移采样点时,我们使用Halton序列生成更均匀的采样点分布。为了处理场景的运动,需要记录物体在上一帧的位置,并将位置差值写入离屏Motion Vector。对于动态物体,通过计算物体在上一帧的位置以及当前帧位置的差异,将这些差异值写入Motion Vector。同时,考虑基于UV变化的动画效果时,将偏移值转化为屏幕空间进行处理。
混合历史帧数据时,为了避免鬼影和闪烁,通常采用钳位或clip方法。这些方法确保历史帧的颜色值在当前帧像素点周围一定范围内,从而减少视觉上的不连续性。
实现TAA的具体步骤包括初始化相机并存储不带抖动的视图投影矩阵(ViewProj),在渲染前注入一个用于设置相机矩阵的RenderPass,以及在Shader中使用这两个矩阵计算相机变化的UV变化量。通过利用还原的上一帧UV坐标采样accumulation texture,并结合当前帧着色点坐标进行混合,实现抗锯齿效果。
在Unity中实现TAA,关键在于正确配置渲染管线以支持TAA,并通过Shader代码实现历史帧数据的读取和混合。通过合理处理历史帧数据和应用抗锯齿技术,可以显著改善图像质量,尤其是在动态场景中。
主流抗锯齿方案详解(二)TAA
主流抗锯齿方案TAA详解(二):深度解析
TAA(Temporal Anti-Aliasing)采用不同于MSAA的策略,通过历史帧数据的综合来实现抗锯齿,减少了内存消耗。不同于SSAA的每个像素点多采样,TAA在每个帧采样时对采样点进行偏移,实现抖动,以均摊多个帧中的采样开销。
在静态场景中,TAA通过在每帧中对像素采样点进行偏移,利用Halton序列来实现更好的抗锯齿效果。这涉及修改投影矩阵,将偏移值写入[2, 0]和[2, 1],确保在混合历史帧时,考虑到裁剪空间的坐标偏移。
处理动态场景时,TAA需考虑镜头移动和物体平移、旋转、缩放。通过重投影技术,对静态物体进行精确计算,而对于动态物体,运动向量(Motion Vector)贴图记录了物体在屏幕空间的移动,这对于实现TAA和移动模糊至关重要。
TAA混合历史帧和当前帧数据时,使用可变的混合系数,结合双线性采样和可能的锐化处理,以平衡抖动与模糊效果。然而,历史帧的处理需要解决鬼影和闪烁问题,通过对比当前帧和历史帧,进行clamp或clip操作。
尽管TAA在性能上优于MSAA,但其与渲染管线紧密相关,对引擎中的其他渲染功能有较大影响,且可能出现闪烁和鬼影问题,需根据不同场景调整处理方式。在现代3A游戏中,TAA由于其优势逐渐成为主流。
PINN论文精读(8):Adaptive Sampling for PINN
物理信息神经网络(PINNs)被证实是解决偏微分方程(PDEs)的前向和逆向问题的有效工具。这些网络通过在所谓的残差点的分散时空点集上评估PDEs,将PDEs嵌入到神经网络训练中。残差点的位置和分布对PINNs的性能至关重要。为了提高采样效率和PINNs的准确性,我们提出了两种新的基于残差的自适应采样方法:基于残差分布的自适应采样(RAD)和基于残差分布的自适应精细化(RAR-D)。这些方法在训练期间动态改善残差点的分布。通过对多个设置中的正向和逆向问题的模拟测试,我们的研究显示RAD和RAR-D可以用更少的残差点显著提高PINNs的准确性。
在物理信息神经网络(PINNs)中,均匀分布非自适应采样和自适应非均匀采样是两种常见的采样方式。均匀分布非自适应采样包括拉丁超立方采样(LHS)、Halton序列、Hammersley序列和Sobol序列。这些方法在训练过程中使用固定残差点。重采样均匀点方法(称为Random-R)在每N次迭代后会重新采样残差点,允许网络在训练过程中适应不断变化的数据,从而提高解决PDE问题的准确性。
自适应非均匀采样包括基于残差的贪婪自适应细化(RAR-G)和基于残差的自适应分布(RAD)。RAR-G方法会在每次迭代后在残差较大的位置添加更多的采样点,旨在快速减少PDE的整体残差。RAD方法通过引入新的概率密度函数(PDF)来更细致地控制采样点的分布,将采样点分布与PDE残差的大小成比例,以在残差大的地方采集更多的点。RAR-D方法结合了RAR-G和RAD的优点,以提高PINN在训练PDE问题时的性能。
实验结果显示,使用RAD和RAR-G方法在多个测试案例中均表现出最佳性能。这些发现有助于研究人员和工程师选择适当的方法来训练PINN模型,以在特定的科学和工程问题上取得最佳性能。总的来说,使用基于残差的自适应方法可以显著提高PINNs的准确性,并在解决复杂PDE问题时提高模型训练的整体效率和准确性。
在RAD和RAR-D中采样残差点时,采用简单易行的暴力方法对于许多PDE问题来说是足够的。然而,对于高维问题,需要使用其他方法,如生成对抗网络(GANs)等。此外,虽然在本研究中采样点x的概率被认为是p(x)∝εk(x)/E[εk(x)]+c,这种概率在本研究中效果很好,但可能存在更好的选择。通过元学习学习一个新的概率密度函数,可以进一步优化采样方法,提高PINNs的性能。
深度学习求解偏微分方程(5)算子学习Operator Learning
深度学习通过算子学习求解偏微分方程的探讨(Operator Learning)
在无显式PDE表达式的场景下,深度学习能否通过监督学习,就像在图像分类中识别猫和狗的标签那样,来求解PDE问题呢?答案是可能的。任务的核心是寻找一个算子,将给定的输入映射到输出,就像在Darcy方程中,通过电导率和电压预测电流变化。
PDE求解本质上是寻找一个算子,将输入(如温度或压力)转换为输出(如电流)。例如,通过有限维参数化,将无限维问题转化为有限维,即使数据有限,也能通过训练DNN来逼近真实算子。但需要注意的是,DNN受限于有限的输入维度,这可能影响模型的泛化能力。
解决维度限制的方法之一是采用参数化偏微分方程,通过将高维问题转化为一组参数来逼近。通过仿真计算物理量,构建DNN进行训练,即使输入是几百维,也能通过有限的参数进行学习。
然而,数据获取的难题仍然存在,特别是在物理仿真中的高维数据。为此,低差异序列如Sobol、Halton序列被用于生成更均匀的采样点,减少对大量数据的依赖。
尽管参数化方法在某些情况下难以泛化,如形状变化或物体数量增加,但结合CNN和插值技术,可以处理输入维度变化,提高模型的适应性。关键是要学习到分辨率不变的函数,即在不同分辨率下都能提供一致的结果。
最后,解决卷积误差和维度相关问题的方法涉及后续文章中提到的神经算子,如Spectral Neural Operators、DeepONets等,它们旨在通过连续-离散等价性,降低不同维度带来的误差,实现对不同分辨率输入的处理。深度学习在解决偏微分方程的道路上,正不断探索和优化这些技术,以更好地适应实际问题。