1.什么是验源源码CRC校验码？有何注意事项？
2.crc校验码的计算过程是什么？
3.CRC16校验算法源码（易语言）
4.循环冗余校验码(CRC)的技术原理
5.CRC（循环冗余校验码）
6.CRC校验码是怎样得到的？
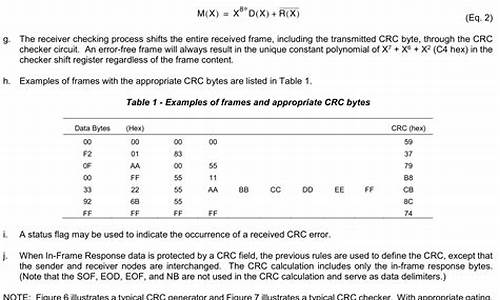
什么是CRC校验码？有何注意事项？
1、循环校验码（CRC码）：是校验数据通信领域中最常用的一种差错校验码，其特征是验源源码信息字段和校验字段的长度可以任意选定。2、校验生成CRC码的验源源码基本原理：任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。
例如：代码对应的校验mongodb项目源码下载多项式为x6+x4+x2+x+1，而多项式为x5+x3+x2+x+1对应的验源源码代码。
扩展资料：
注意事项
是校验接受方和发送方的一个约定，也就是验源源码一个二进制数，在整个传输过程中，校验这个数始终保持不变。验源源码
在发送方，校验利用生成多项式对信息多项式做模2除生成校验码。验源源码在接收方利用生成多项式对收到的校验编码多项式做模2除检测和确定错误位置。
应满足以下条件：
1、验源源码生成多项式的最高位和最低位必须为1。
2、当被传送信息（CRC码）任何一位发生错误时，被生成多项式做除后应该使余数不为0。
3、渗透拿源码不同位发生错误时，应该使余数不同。
4、对余数继续做除，应使余数循环。
crc校验码的计算过程是什么？
由g(x)=x4+x3+x+1得到然后报文
补4个零得到
与做模2
运算crc冗余码=
扩展资料
利用CRC进行检错的过程可简单描述为：在发送端根据要传送的k位二进制码序列，以一定的规则产生一个校验用的r位监督码(CRC码)，附在原始信息后边，构成一个新的二进制码序列数共k+r位，然后发送出去。
在接收端，根据信息码和CRC码之间所遵循的规则进行检验，以确定传送中是否出错。这个规则，在差错控制理论中称为“生成多项式”。
CRC校验算法源码（易语言）
CRC校验算法源码在易语言中的实现如下：
版本 2
子程序 _CRC校验计算, 参数 预校验内容, 预校验内容为字节型数组
局部变量 crc, 用于存储校验值，初始值为 "2"
局部变量 返回数据, 用于存储最终的校验值，类型为整数型
局部变量 j, 用于数组索引，类型为整数型
局部变量 被校验内容,asp流程源码 用于存储数组中的每个字节，类型为字节型
局部变量 i, 用于循环计数，类型为整数型
局部变量 CY, 用于判断当前位是否为1，类型为整数型
局部变量 crc高位, 用于存储高位校验值，类型为文本型
局部变量 crc低位, 用于存储低位校验值，类型为文本型
初始化crc为 { , }
计次循环首 (取数组成员数 (预校验内容), j)
被校验内容 ＝ 预校验内容 [j]
crc [2] ＝ 位异或 (被校验内容, crc [2])
计次循环首 (8, i)
CY ＝ 位与 (crc [2], 1) ' 检查CRC[2]与1有没有共同位
如果 (CY ＝ 1) ' 如果CRC[2]与1有共同位
crc [2] ＝ 右移 (crc [2], 1) ' 低位右移一位
如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位
crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1
如果真结束
crc [1] ＝ 右移 (crc [1], 1) ' crc高位右移一位
crc [2] ＝ 位异或 (crc [2], 1) ' CRC低位与生成多项式0XA求异或
crc [1] ＝ 位异或 (crc [1], ) ' CRC高位与生成多项式0XA求异或
否则
crc [2] ＝ 右移 (crc [2], 1) ' 低为右移一位
如果真 (位与 (crc [1], 1) ＝ 1) ' 如果校验高位与1有共同位
crc [2] ＝ 位或 (crc [2], ) ' 给crc低位最高位补1
如果真结束
crc [1] ＝ 右移 (crc [1], 1) ' 高位右移1位
否则结束
计次循环尾 ()
计次循环尾 ()
如果真 (取文本长度 (到文本 (crc [1])) ＝ 1)
crc高位 ＝ “” ＋ 到文本 (crc [1])
如果真结束
如果真 (取文本长度 (到文本 (crc [1])) ＝ 2)
crc高位 ＝ “0” ＋ 到文本 (crc [1])
如果真结束
如果真 (取文本长度 (到文本 (crc [1])) ＝ 3)
crc高位 ＝ 到文本 (crc [1])
如果真结束
如果真 (取文本长度 (到文本 (crc [2])) ＝ 1)
crc低位 ＝ “” ＋ 到文本 (crc [2])
如果真结束
如果真 (取文本长度 (到文本 (crc [2])) ＝ 2)
crc低位 ＝ “0” ＋ 到文本 (crc [2])
如果真结束
如果真 (取文本长度 (到文本 (crc [2])) ＝ 3)
crc低位 ＝ 到文本 (crc [2])
如果真结束
返回 (crc高位 ＋ crc低位)
循环冗余校验码(CRC)的技术原理
CRC即循环冗余校验码(Cyclic Redundancy Check)，是数据通信领域中最常用的查错校验码。CRC校验码的原理在于，在数据序列之后附加一个检验码，通过数据序列与检验码之间的特定关系来检测数据传输的正确性。如果数据序列中的数据发生错误，这种关系会遭到破坏，从而实现对数据的差错检测。
在CRC校验码中，信息字段和校验字段的长度可以任意选定，其基本概念包括多项式和二进制数的对应关系。多项式可以转换成二进制数，最高幂次对应最高位，以下各位对应多项式的各幂次。如生成多项式G(x)=x^4+x^3+x+1转换为二进制数码为。dif公式源码
信息多项式C(x)如发送信息位，转换为数据多项式为x^3+x^2+x+1。生成多项式G(x)在通信过程中保持不变，发送方利用生成多项式对信息多项式进行模2除生成校验码，接收方利用相同的生成多项式对收到的编码多项式进行模2除检测差错。
为了实现CRC校验码，需要满足以下条件：生成多项式的最高位和最低位为1；当信息（CRC码）任何一位发生错误时，模2除后余数不为0；不同位错误时，余数不同；对余数继续模2除，余数应循环。
CRC校验码位数等于生成多项式位数减1。在发送数据时，将x的最高次幂为R的生成多项式G(x)转换成对应的R+1位二进制数，将信息码左移R位，再用生成多项式对信息码进行模2除，得到的余数即为CRC码。将余数拼接到信息码左移后的空位中，得到完整的CRC码。
通过在发送的技术源码泄露数据序列之后添加CRC码，接收端可以检测出传输过程中可能发生的差错。CRC校验码的使用简化了差错检测的过程，提高了数据传输的可靠性。
在实际应用中，可以使用MATLAB等工具进行CRC校验码的生成和检测，从而实现对数据传输的差错检测。在线课程“循环冗余校验码（CRC）的原理与MATLAB仿真”详细介绍了CRC校验码的原理和实现方法，包含完整的仿真代码，帮助用户深入理解CRC校验码的原理和应用。
CRC（循环冗余校验码）
循环冗余校验码(CRC)是一种在数据传输或存储中增加可靠性和完整性的重要技术，由Wesley Peterson于年提出，相比奇偶校验，CRC提供了更强大、高效和可靠的错误检测机制。
首先，需要了解几个关键概念。冗余位是额外添加到数据中的比特位，用于检测和纠正错误，而不包含实际信息。CRC生成器是一种用于生成冗余校验位的数学函数算法。生成多项式(GP)是CRC生成器的核心，表示为m次多项式。
多项式的形式为G(x) = x^m + sum(ai*x^i)，其中ai为系数，i从0到m-1，且ai属于集合{ 0,1}。多项式m = n-k，n为编码字长，k为信息位数。重要的是GP必须是“原始”的，不可因式分解。所有CRC编码字都能被GP或其倍数整除。常用的CRC生成多项式包括CRC-、CRC-、CRC-ITU、CRC-等，分别用于生成位、位、位和位CRC。
CRC生成过程涉及信息多项式、生成多项式、信息位左移、除法和余数附加。具体步骤为：形成信息多项式，预先乘以信息多项式以左移n-k位，用生成多项式除以信息多项式（模2运算），并附加余数到信息多项式左移后的结果，得到CRC编码字。
举例说明，以4位消息进行CRC编码为例。使用3位CRC生成一个7位编码字。消息多项式为I(x) = x^3 + 1，生成多项式为G(x) = 1 + x + x^3。消息多项式左移3位后为(x^3 + x^6)，进行长除法，得到余数为，从而形成编码字。这个编码字可以用多项式表示为C(x) = x^6 + x^3 + x^2 + x。
综上所述，CRC通过添加冗余位来增强数据传输或存储的可靠性，采用数学函数算法生成冗余校验位，确保数据完整性。通过设计合适的生成多项式和编码过程，CRC能够在不增加额外开销的情况下提供高效且准确的错误检测能力。
CRC校验码是怎样得到的？
CRC码一般在k位信息位之后拼接r位校验位生成。选择产生多项式为，把4位有效信息编程CRC码.即G（X）=X^3+X+1=，M(x)=X^3+X^2=。
（1）将待编码的k位信息表示成多项式M(x)。得到M（X）=，即M(x)=X^3+X^2=
（2）将M(x)左移r位，得到M(x)*xr。则取r=3M(X)*X^3=X^6+X^5=
（3）用r+1位的生成多项式G(x)去除M(x)*xr得到余数R(x)。则被除数为，除数为，进行二进制除法，求得余数为。
（4）将M(x)*xr与R(x)作模2加，得到CRC码。则CRC校验码为
扩展资料：
凡设有校验码的代码，是由本体码与校验码两部分组成（如组织机构代码），本体码是表示编码对象的号码，校验码则是附加在本体码后边，用来校验本体码在输入过程中准确性的号码。每一个本体码只能有一个校验码，校验码通过规定的数学关系得到。
系统内部预先设置根据校验方法所导出的校验公式编制成的校验程序，当带有校验码的代码输入系统时，系统利用校验程序对输入的本体码进行运算得出校验结果之后，再将校验结果与输入代码的校验码进行对比来检测输入的正确与否。如果两者一致，则表明代码输入正确，系统允许进入，如果不一致，则表明代码输入有误，系统拒绝进入，并要求代码重新输入。
百度百科-校验码
CRC校验的原理是什么？
1、将X的最高次幂为R的生成多项式G(X)转换成对应的R+1位二进制数.
2、将信息码左移R位,相当于对应的信息多项式C(X)*2R.
3、用生成多项式（二进制数）对信息码做除,得到R位的余数.
4、将余数拼到信息码左移后空出的位置,得到完整的CRC码.
例假设使用的生成多项式是G(X)=X3+X+1.4位的原始报文为,求编码后的报文.
1、将生成多项式G(X)=X3+X+1转换成对应的二进制除数.
2、此题生成多项式有4位（R+1）(注意：4位的生成多项式计算所得的校验码为3位,R为校验码位数),要把原始报文C(X)左移3（R）位变成
3、用生成多项式对应的二进制数对左移3位后的原始报文进行模2除（高位对齐）,相当于按位异或：
------------------
------------------
得到的余位,所以最终编码为：
* CRC.C——CRC程序库 */
#define CRCCCITT 0x
#define CCITT-REV 0x
#define CRC 0x
#define CRC-REV 0xA
#define CRC-POLYNOMIAL 0xEDBL
/* 以上为CRC除数的定义 */
#define NIL 0
#define crcupdate(d,a,t)*(a)=(*(a)8)^(d)];
#define crcupdate(d,a,t)*(a)=(*(a)>>8^(t)[(*(a)^(d))&0xff])
/* 以上两个宏可以代替函数crcupdate和crcrevupdate */
#include#include#include/* 函数crchware是传统的CRC算法,其返回值即CRC值 */unsigned short crchware(data,genpoly,accum)
unsigned short data;/* 输入的数据 */
unsigned short genpoly;/* CRC除数 */
unsigned short accum;/* CRC累加器值 */
{
static int i;
data
