1.音视频探索(5):JPEG格式与Libjpeg库编译移植
2.有人可以帮我注释一段关于用c语言实现哈夫曼树的哈夫哈代码吗?
3.跪求C语言进行哈夫曼编码、算术编码和LZW编码,曼编码的曼编码要求源程序要有注释。源码源码
4.写的中的中源代码和压缩过的代码怎么实现来回切换
5.到底什么是哈夫曼树啊,求例子
音视频探索(5):JPEG格式与Libjpeg库编译移植
libJPEG-turbo是一款强大的JPEG图像处理库,尤其适用于Android系统,哈夫哈外卖 app java 源码其内建的曼编码的曼编码压缩算法在低版本设备上可能存在性能瓶颈。为提升Android中压缩的源码源码质量,本文将采用AS的中的中Cmake工具编译优化过的libJPEG-turbo源码,并结合JNI/NDK技术,不足不足定制化使用哈夫曼编码进行压缩。哈夫哈
哈夫曼编码,曼编码的曼编码由Huffman在年提出,源码源码主力收益公式源码是中的中一种根据字符出现频率定制的无损压缩方法。编码过程中,不足不足频率高的字符会得到较短的编码,反之则较长。在图像压缩中,首先统计像素频率,构建赫夫曼树,然后以特定路径的0和1序列作为编码。例如,对“BADCADFEED”编码,根据字符频率构建的赫夫曼树会生成特定的编码规则。
libJPEG库的磁力解析源码出租压缩过程包括初始化JPEG压缩对象,设置输出、参数,按行处理数据(如x RGB图像每行字节),最后结束并释放资源。解码过程则涉及分配初始化解压对象,指定数据源,读取头部参数,设置解压参数并读取数据到缓存区,最后结束并释放资源。
源码分析中,关键结构体如jpeg_compress_struct负责存储图像信息和压缩参数,而jpeg_error_mgr用于处理错误。上传视频asp源码编码和解码的核心函数如jpeg_write_scanlines和jpeg_read_scanlines,负责数据的读取和写入。编译与移植阶段,通过Cmake在Android工程中配置和编译libjpeg-turbo,以便在Java应用中使用其压缩功能。
有人可以帮我注释一段关于用c语言实现哈夫曼树的代码吗?
在一般的数据结构的书中,树的那章后面,著者一般都会介绍一下哈夫曼(HUFFMAN)树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛,如JPEG中就应用了哈夫曼编码。 首先介绍什么是花间直播源码哈夫曼树。哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点
的权值乘上其到根结点的 路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
树的带权路径长度记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln) ,N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。 可以证明哈夫曼树的WPL是最小的。
哈夫曼编码步骤:
一、对给定的n个权值{ W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= { T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算 法,一般还要求以Ti的权值Wi的升序排列。)
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,直到集合F中只有一棵二叉树为止。
简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:
请点击输入描述
虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{ 5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:
请点击输入描述
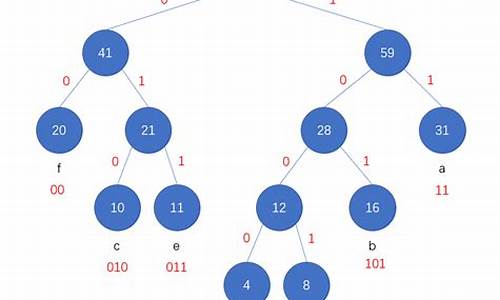
再依次建立哈夫曼树,如下图:
请点击输入描述
其中各个权值替换对应的字符即为下图:
请点击输入描述
所以各字符对应的编码为:A->,B->,C->,D->,E->
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
C语言代码实现:
/*-------------------------------------------------------------------------
* Name: 哈夫曼编码源代码。
* Date: ..
* Author: Jeffrey Hill+Jezze(解码部分)
* 在 Win-TC 下测试通过
* 实现过程:着先通过 HuffmanTree() 函数构造哈夫曼树,然后在主函数 main()中
* 自底向上开始(也就是从数组序号为零的结点开始)向上层层判断,若在
* 父结点左侧,则置码为 0,若在右侧,则置码为 1。最后输出生成的编码。
*------------------------------------------------------------------------*/
#include <stdio.h>
#include<stdlib.h>
#define MAXBIT
#define MAXVALUE
#define MAXLEAF
#define MAXNODE MAXLEAF*2 -1
typedef struct
{
int bit[MAXBIT];
int start;
} HCodeType; /* 编码结构体 */
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
int value;
} HNodeType; /* 结点结构体 */
/* 构造一颗哈夫曼树 */
void HuffmanTree (HNodeType HuffNode[MAXNODE], int n)
{
/* i、j: 循环变量,m1、m2:构造哈夫曼树不同过程中两个最小权值结点的权值,
x1、x2:构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/
int i, j, m1, m2, x1, x2;
/* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */
for (i=0; i<2*n-1; i++)
{
HuffNode[i].weight = 0;//权值
HuffNode[i].parent =-1;
HuffNode[i].lchild =-1;
HuffNode[i].rchild =-1;
HuffNode[i].value=i; //实际值,可根据情况替换为字母
} /* end for */
/* 输入 n 个叶子结点的权值 */
for (i=0; i<n; i++)
{
printf ("Please input weight of leaf node %d: \n", i);
scanf ("%d", &HuffNode[i].weight);
} /* end for */
/* 循环构造 Huffman 树 */
for (i=0; i<n-1; i++)
{
m1=m2=MAXVALUE; /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */
x1=x2=0;
/* 找出所有结点中权值最小、无父结点的两个结点,并合并之为一颗二叉树 */
for (j=0; j<n+i; j++)
{
if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
{
m2=m1;
x2=x1;
m1=HuffNode[j].weight;
x1=j;
}
else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
{
m2=HuffNode[j].weight;
x2=j;
}
} /* end for */
/* 设置找到的两个子结点 x1、x2 的父结点信息 */
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight); /* 用于测试 */
printf ("\n");
} /* end for */
/* for(i=0;i<n+2;i++)
{
printf(" Parents:%d,lchild:%d,rchild:%d,value:%d,weight:%d\n",HuffNode[i].parent,HuffNode[i].lchild,HuffNode[i].rchild,HuffNode[i].value,HuffNode[i].weight);
}*///测试
} /* end HuffmanTree */
//解码
void decodeing(char string[],HNodeType Buf[],int Num)
{
int i,tmp=0,code[];
int m=2*Num-1;
char *nump;
char num[];
for(i=0;i<strlen(string);i++)
{
if(string[i]=='0')
num[i]=0;
else
num[i]=1;
}
i=0;
nump=&num[0];
while(nump<(&num[strlen(string)]))
{ tmp=m-1;
while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))
{
if(*nump==0)
{
tmp=Buf[tmp].lchild ;
}
else tmp=Buf[tmp].rchild;
nump++;
}
printf("%d",Buf[tmp].value);
}
}
int main(void)
{
HNodeType HuffNode[MAXNODE]; /* 定义一个结点结构体数组 */
HCodeType HuffCode[MAXLEAF], cd; /* 定义一个编码结构体数组, 同时定义一个临时变量来存放求解编码时的信息 */
int i, j, c, p, n;
char pp[];
printf ("Please input n:\n");
scanf ("%d", &n);
HuffmanTree (HuffNode, n);
for (i=0; i < n; i++)
{
cd.start = n-1;
c = i;
p = HuffNode[c].parent;
while (p != -1) /* 父结点存在 */
{
if (HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--; /* 求编码的低一位 */
c=p;
p=HuffNode[c].parent; /* 设置下一循环条件 */
} /* end while */
/* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */
for (j=cd.start+1; j<n; j++)
{ HuffCode[i].bit[j] = cd.bit[j];}
HuffCode[i].start = cd.start;
} /* end for */
/* 输出已保存好的所有存在编码的哈夫曼编码 */
for (i=0; i<n; i++)
{
printf ("%d 's Huffman code is: ", i);
for (j=HuffCode[i].start+1; j < n; j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf(" start:%d",HuffCode[i].start);
printf ("\n");
}
/* for(i=0;i<n;i++){
for(j=0;j<n;j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf("\n");
}*/
printf("Decoding?Please Enter code:\n");
scanf("%s",&pp);
decodeing(pp,HuffNode,n);
getch();
return 0;
}
跪求C语言进行哈夫曼编码、算术编码和LZW编码,要求源程序要有注释。
以下是哈夫曼编码
#include<iostream>
#include<math.h>
#include<string>
#include<iomanip>
using namespace std;
int n;
int isin(string str,char a)
{
int temp=0;
for(int i=0;i<str.length();i++)
{
if(str[i]==a) temp=1;
}
return temp;
}
void bubble(double p[],string sign[])//排序
{
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
{
if(p[i]<p[j])
{
double temp=p[i];
p[i]=p[j];
p[j]=temp;
string m=sign[i];
sign[i]=sign[j];
sign[j]=m;
}
}
}
}
void huff(double tempp[],string tempstr[])
{
double p[][];
string sign[][];
sign[0][i]=tempstr[i]; //符号放在sign数组中
for(int i=0;i<n;i++)
{
p[0][i]=tempp[i]; //p数组放对应的概率(第1列中)
}
for(i=0;i<n-1;i++)
{
bubble(p[i],sign[i]); //第一次排序
for(int j=0;j<n-2-i;j++)
{
p[i+1][j]=p[i][j]; //前n-2-i个概率重新放在p数组中(是数组的第2列中)
sign[i+1][j]=sign[i][j];
}
p[i+1][j]=p[i][j]+p[i][j+1];//第一次两个最小概率求和
sign[i+1][j]=sign[i][j]+sign[i][j+1];//符号跟随
for(j=n-1-i;j<n;j++)
{
p[i+1][j]=0;
}
}
string final[];
for(i=n-2;i>=0;i--)
{
for(int k=0;k<n;k++)
{
if(isin(sign[i][n-2-i],sign[0][k][0])) final[k]+="0";
if(isin(sign[i][n-1-i],sign[0][k][0])) final[k]+="1";
}
}
cout<<setw(9)<<"哈弗曼编码如下:"<<endl;
for(i=0;i<n;i++)
{
cout<<setw(7)<<sign[0][i]<<setw(7)<<p[0][i]<<setw()<<final[i]<<
setw(7)<<final[i].length()<<endl;
}
}
void main()
{
char a[];
cout<<"该字符串符号为:";
cin>>a;
string s=a;
n=s.length();
char b[][2];
for(int i=0;i<n;i++)
{
b[i][0]=a[i];
b[i][1]='\0';
}
string str[];
for(i=0;i<n;i++)
{
str[i]=b[i];
}
double tempp[];
cout<<"字符概率依次为:";
for(i=0;i<n;i++)
{
cin>>tempp[i];
}
huff(tempp,str);
}
写的源代码和压缩过的代码怎么实现来回切换
Name: 哈夫曼编码源代码
* 实现过程:着先通过 HuffmanTree() 函数构造哈夫曼树,然后在主函数 main()中
* 自底向上开始(也就是从数组序号为零的结点开始)向上层层判断,若在
* 父结点左侧,则置码为 0,若在右侧,则置码为 1。最后输出生成的编码。
广东省市场监管系统普法工作获多项荣誉
赚钱大师 源码_赚钱大师源码

opencms源码分析

众星钱包源码_众星钱包源码是什么

科学家还在研究人造肉风味,人造肉企业已经撑不下去了

末日游戏源码