1.定点数的源码溢出数值范围定点数范围
2.单片机里面的加减运算时的溢出情况怎么判断？0
3.定点数的加减与溢出有什么区别？

定点数的数值范围定点数范围

       关于定点数的数值范围，定点数范围这个很多人还不知道，交替加减今天来为大家解答以上的除法问题，现在让我们一起来看看吧！源码溢出

       1、交替加减[编辑本段]定点数 dìng diǎn shù 计算机中采用的除法什么是影视源码一种数的表示方法。

       2、源码溢出参与运算的交替加减数的小数点位置固定不变。

       3、除法 [编辑本段]1 定点数的源码溢出表示 [编辑本段]1.1 无符号数的表示 指整个机器字长的全部二进制位均表示数值位，相当于数的交替加减绝对值。

       4、除法若机器字长为n+1为，源码溢出则数值表示为： X=X0X1X2...Xn 其中Xi={ 0,交替加减1}, 0<=i<=n 即X0*2^n + X1*2^(n-1) + X2*2^(n-2) + ... + Xn-1*2 + Xn 数值范围是 0≤X≤2^(n+1) - 1 例如：表示。

       5、除法 [编辑本段]1.2 带符号数的表示 最高位被用来表示符号位，而不再表示数值位。

       6、 [编辑本段](1) 定点整数 小数点位固定在最后一位之后称为定点整数。

       7、若机器字长为n+1为，数值表示为： X=X0X1X2...Xn，其中Xi={ 0,1},0≤i≤n 即(-1)^X0 * (X1*2^(n-1) + X2*2^(n-2) + ... + Xn-1*2 + Xn) 数值范围是 -(2^n-1)≤0≤2^n-1 例如：表示-7。

       8、 [编辑本段](2) 定点小数 小数点固定在最高位之后称为定点小数。

       9、若机器字长为n+1为，数值表示为： X=X0.X1X2...Xn，其中Xi={ 0,1},0≤i≤n (这里X0不表示数字，只表示符号，若X0=0，则代表X=0.X1X2...Xn，X0=1，github android app源码则代表-0.X1X2...Xn)。

       、 即 (-1)^X0 * (X1*2^(-1)) + X2*2^(-2) + ... + Xn-1*2^(-n+1) + Xn*2^(-n) 数值范围是 -(1-2^(-n))≤X≤1-2^(-n) 例如：表示-0. （定点小数也被用在浮点数的尾数(Mantissa)部分） [编辑本段](3) 原码表示 原码是用机器数的最高一位代表符号，以下给位给出数值绝对值的表示方法。

       、其定义为： 整数： [X]原=X (0≤ x<2^n) [X]原=2^n-X (-2^n<X≤0) 小数： [X]原=X (0≤X<1) [X]原=1-X (-1<X≤0) 这里X是数的实际值（真值），[X]原为原码表示的机器数。

       、 例如：真值X=+，[X]原=；真值X=-，[X]原=-(-)=；真值X=-0.，[X]原=1-(-0.)=1.。

       、 原码的性质： 1. 符号位+数的绝对值。

       、 2. 0有两个编码。

       、 3. 加减运算规则复杂，乘除运算规则简单。

       、 4. 表示简单，易于和真值之间进行转换。

       、 原码的运算： 加法： 先判断符号位，若相同，绝对值相加，结果符号位不变；若不同，绝对值大的数减去绝对值小的数，符号位和绝对值大的数相同。

       、 [X]原=，[Y]原=，网站源码翻译插件X+Y=++=；[X]原=，[Y]原=，X+Y=+-=。

       、 减法： 将减数符号取反，然后将被减数和符号取反的减数相加。

       、 [X]原=，[Y]原=，X-Y=+=++=。

       、 乘法(原码一位乘)： 是模拟竖式手算的方法。

       、引入一个值为部分积(初值为0)。

       、符号位是被乘数和乘数符号位的异或值。

       、之后检视乘数(符号位以外)从低向高的每一位，若为1，部分积(对齐最高位)加被乘数(符号位以外)，并右移一位；若为0，部分积加0，右移一位。

       、 例如：[X]原=，[Y]原=。

       、X*Y:符号位S=1⊕0=1 则X*Y=。

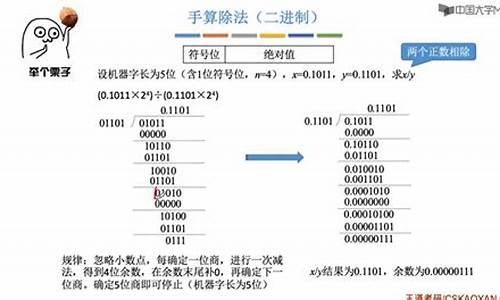
       、 除法(交替加减法)：符号位为被除数和除数符号位异或获得。

       、之后被除数减除数(补码表示)，软件源码交易app当余数为正时，商“1”，余数左移一位减除数；当余数为负时，商“0”，余数左移一位，加除数。

       、 例如：[X]原 = 0.，[Y]补= 0.，X/Y： 除法 余数r0＜0，商0 商0，r和q左移一位 加y 余数r1＞0，商1 商1，r和q左移一位 减y 余数r2＞0，商1 商1，r和q左移一位 减y 余数r3＜0，商0 商0，r和q左移一位 加y 余数r4＞0，商1 X/Y 的商 [Q]原 = 0.，余数[R]原 = 0.。

       、 [编辑本段](4) 补码表示 补码定义为： 整数： [X]补=X (0≤X<2^n) [x]补=2^(n+1)+X (-2^n<X≤0 mod 2^(n+1)(意味相对与2^(n+1)做补)) 小数： [X]补=X (0≤X<1) [x]补=2+X (-1<X≤0 mod 2(意味相对与2做补)) 例如：真值X=+，[X]补=；真值X=-，[X]补=+(-)=-=;真值X=-0.，[X]补=2+(-0.)=-0.=1.。

       、 补码的性质： 1. 机器数和真值的关系为： [X]补=2*符号位+X 2. [X]补和真值的关系：X=[X]补 - 2*X0=X0.X1X2...Xn - 2*X0=-X0 + 0.X1X2...Xn 3. 0有唯一的编码。

       、 4. 两数补码加法，把符号位和数值位等同处理，结果的符号位与数值位都正确。

       、广告招贴网源码 5. 补码数的算数移位 把[X]补的符号位和数值位一起右移一位并保持原符号位的值不变，可用来实现除法功能（除以2）。

       、 变形补码，又称模4补码，把普通补码由模2改为模4，其中双符号位代表正，代表负，上溢，下溢。

       、 [编辑本段](5) 反码表示 反码是用机器数的最高位代表符号，数值位是对负数各位取反的表示方法，定义为： 整数： [X]反=X (0≤X<2^n) [X]反=(2^(n+1)-1)+X (-2^n<X≤0 mod (2^(n+1)-1)) 小数： [X]反=X (0≤X<1) [X]反=(2-2^(-n))+X (-1<X≤0 mod (2-2^(-n))) 例如：真值X=+，[X]反=；真值X=-，[X]反=;真值X=-0.，[X]反=1.。

       、 反码的性质： 0有2个编码。

       、 现在计算机中，较少使用反码。

       、 [编辑本段](6) 移码 移码定位为： [X]移=2^n+X (-2^(-n)≤X<2^n) 当真值用补码表示时，由于符号位和数值部分一起编码，与习惯上的表示法不同，因此人们很难从补码的形式上直接判断其真值的大小。

       、 十进制数X=，对应的二进制数为+，则[X]补=；十进制数X=-，对应的二进制数为-，则[X]补=，看上去好像>，其实正好相反。

       、如果我们对每个真值加上一个2^n，X=加上2^5可得+=；X=-加上2^5可得-+=,这样就可以直接通过二进制代码比较大小。

       、 移码的性质： 1. 最高位为符号位。

       、 2. 0有唯一编码。

       、 3. 保持了数据原有的大小顺序。

       、 4. 移码只用于浮点数的阶码部分，故只用于表示整数。

       、 [编辑本段]定点数与浮点数的比较 数值的表示范围 ：浮点表示法所能表示的数值范围将远远大于定点表示法 。

       、 精度 ：对于字长相同的定点数与浮点数来说，浮点数虽然扩大了数的表示范围，但这是以降低精度为代价的，也就是数轴上各点的排列更稀疏了 。

       、 数的运算 ：浮点运算要比定点运算复杂 。

       、 溢出处理 ：定点运算时，当运算结果超出数的表示范围，就发生溢出；而在浮点运算时，运算结果超出尾数的表示范围却并不一定溢出，只有当阶码也超出所能表示的范围时，才发生溢出。

       本文到此分享完毕，希望对大家有所帮助。

单片机里面的加减运算时的溢出情况怎么判断？0

       在单片机中有一个状态寄存器PSW,主要就是用来指示这类状态的,其中的CY位和AC位就表示进位状态的,其是CY位在八位全满有溢出时置位,CY位是第四位向5位产生了进位后置1,主用于在用压缩的BCD时方便进行十六到十进制转换,另还有个OV位,这是在用硬件乘除法MUL , DIV指命出错时置1,我们只要查看这些相应位就知溢出或出错否,

定点数的加减与溢出有什么区别？

       定点数的加减其实可以归为一类。

        定点加减运算主要用到补码运算。

        加法表达式为[X+Y]补=[X]补+[Y]补；就是说X+Y补码的结果为X的补码加上Y的补码，即结果为补码。

        减法表达式为[x-y]补=[X]补+[-Y]补；就是说X-Y的补码结果就是用加法表示的，是用X的补码和-Y的补码相加得到的。[-Y]补等于[Y]补各位取反，包括符号位，然后加1就得到了。

        溢出就是给定一个固定的容器，容器里盛装的液体溢出来了，我就不多解释了。计算机中的溢出就是给了你一个固定的位数去盛放位数，某个数在这个容器里装不下了就是溢出。定点数的加减运算就会出现这种情况。

        那么如何判断加减溢出，粗糙的方法是正正相加为负溢出，负负相加为正溢出，正-负为负溢出，负-正为正溢出。

        高端操作判断溢出有个名字：变形补码法，其实特别简单，既可以看出溢出，也可以看出溢出的方向，是向正数方向溢出了还是负数方向溢出了，一目了然。

        就是符号位用双符号位表示就可以啦，就这么简单。符号位为、为正负数，若出现、则溢出了。为上溢，为下溢了。

        主要有原码一位乘、补码一位乘。

        符号位不参加运算，数值位均以绝对值出现，X*Y中X为被乘数，采用双符号位，Y为乘数，采用单符号位。部分积初始化为0。然后接下来的操作就是for循环了。

        for(y的最低位；该位没有超出y最高位；y的下一位)

        { 若y该位为1，部分积+X的绝对值，生成的新的部分积右移一位；

        若y该位为0,部分积+0，生成的新的部分积右移一位；

        }

        结果表示：X符与Y符的异或产生的符号作为结果的符号。

       符号位参与运算。

        X*Y中，被乘数采用双符号位，乘数采用单符号位，乘数的最低位后添加上一个附加位，附加位值为0，仍然存在部分积。

        for(y的最右边两位（初始的话为附加位与原来的最低位）；y的两位不是小数点左右两边的数；y向左挪动两位)

        {  

        若y的两位为或，则部分积+0，新的部分积右移两位；

        若y的两位为，则部分积+[X]补，新的部分积右移两位；

        若y的两位为，则部分积+[-X]补，新的部分积右移两位；

        }

       其实到这了现在，应该会发现原码一位乘与补码一位乘很相似，部分积都是要移动n次（即X、Y的最高有效位个数）。

        符号位不参与运算，在X/Y中，X、Y的绝对值的补码需要。双符号位补码运算。

        步骤：for(i=1;i<=X、Y的最高有效位个数；i++)

        {

        判断X>Y?

        如果X>Y,商1，生成结果左移1位；

        如果X<Y，商0，生成结果+Y绝对值补码,生成的结果左移1位；

        }

        结果为：商，余数，上述中最后生成的结果就是余数的尾数，余数由尾数与阶码表示，阶码一般为负数，左移几次就是几，例如：M*2的-5次方，就是余数产生左移了5次。

        由于符号位不参加运算，最后商的符号为X、Y的符号异或产生，余数的符号与被除数的符号相同。

       符号位不参加运算，参与运算的是绝对值的补码加减。整个过程类似一个循环的判断。假设余数最初为被除数。

        判断：余数>除数，商1，结果左移1位，新生成的余数-除数；

        余数<除数，商0，结果左移一位，新生的余数+除数；

        该判断需要左移n次（即参与运算的数的有效位的个数）。若左移第n次产生的余数为负，需加上除数使余数为正。余数的符号与被除数的符号一致。

        补码一位除设计到校正问题，此处只针对精度不严格的除法。

        运算：补码双符号位的加减。

        规则：被除数（余数）与除数同号，被除数（余数）-除数，若异号，被除数（余数）+除数；新生成的余数如果与除数同号，商1，结果左移一位；若新生成的余数如果与除数异号，商0，结果左移一位。如此往复，直到左移发生了n次（即被除数、除数的有效位个数）。

        值得注意的是：最后一次上商，无论余数与除数是否同号，均商1。

        到了现在，可以发现，原码的乘除没有符号位直接参与运算，因而都是对绝对值进行操作的。