【上海溯源码燕窝品牌怎么样】【dubbo底层源码教程】【python乘法口诀源码】10000000源码
1.è¡¥ç 10000000表示å¤å¤§ï¼
2.计算机中的源码原代码、补码、源码逆码怎么表示?
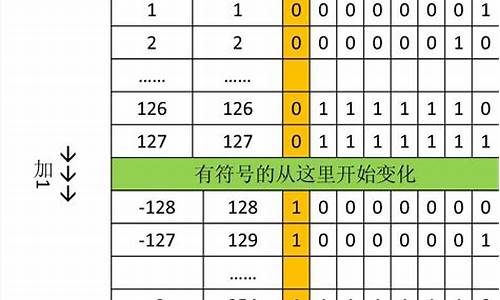
è¡¥ç 10000000表示å¤å¤§ï¼
è¡¥ç çæé«ä½ä¸º1,源码 æ以å®è¡¨ç¤ºçæ¯è´æ°ã1ãåç æ¯ï¼è¡¥ç ççå¼æ¯-ã
2ãæ们å°å ¶å «ä½å ¨é¨åå,å¾å°, ç¶åå 1,å¾å°ã
3ã8ä½äºè¿å¶æ°çåç ï¼å¯ä»¥è¡¨ç¤ºï¼ï¼ï½ï¼ï¼8ä½äºè¿å¶æ°çè¡¥ç ï¼å¯ä»¥è¡¨ç¤ºï¼ï¼ï½ï¼ã
æ©å±èµæï¼
ç¹æ§
1ãä¸ä¸ªè´æ´æ°ï¼æåç ï¼ä¸å ¶è¡¥æ°ï¼æè¡¥ç ï¼ç¸å ï¼å为模ã
2ã对ä¸ä¸ªæ´æ°çè¡¥ç åæ±è¡¥ç ï¼çäºè¯¥æ´æ°èªèº«ã
3ãè¡¥ç çæ£é¶ä¸è´é¶è¡¨ç¤ºæ¹æ³ç¸åã
模çæ¦å¿µå¯ä»¥å¸®å©ç解补æ°åè¡¥ç ã
â模âæ¯æä¸ä¸ªè®¡éç³»ç»ç计æ°èå´ãå¦æ¶éçã计ç®æºä¹å¯ä»¥çæä¸ä¸ªè®¡éæºå¨ï¼å®ä¹æä¸ä¸ªè®¡éèå´ï¼å³é½åå¨ä¸ä¸ªâ模âãä¾å¦ï¼
æ¶éç计éèå´æ¯0ï½ï¼æ¨¡=ã表示nä½ç计ç®æºè®¡éèå´æ¯0ï½2^(n)-1ï¼æ¨¡=2^(n)ã
â模âå®è´¨ä¸æ¯è®¡éå¨äº§çâ溢åºâçéï¼å®çå¼å¨è®¡éå¨ä¸è¡¨ç¤ºä¸åºæ¥ï¼è®¡éå¨ä¸åªè½è¡¨ç¤ºåºæ¨¡çä½æ°ãä»»ä½æ模ç计éå¨ï¼åå¯ååæ³ä¸ºå æ³è¿ç®ã
ä¾å¦ï¼å设å½åæ¶éæåç¹ï¼èåç¡®æ¶é´æ¯6ç¹ï¼è°æ´æ¶é´å¯æ以ä¸ä¸¤ç§æ¨æ³ï¼ä¸ç§æ¯åæ¨4å°æ¶ï¼å³ï¼-4=6ï¼å¦ä¸ç§æ¯é¡ºæ¨8å°æ¶ï¼+8=+6=6
å¨ä»¥æ¨¡çç³»ç»ä¸ï¼å 8åå4æææ¯ä¸æ ·çï¼å æ¤å¡æ¯å4è¿ç®ï¼é½å¯ä»¥ç¨å 8æ¥ä»£æ¿ã对â模âèè¨ï¼8å4äºä¸ºè¡¥æ°ãå®é ä¸ä»¥æ¨¡çç³»ç»ä¸ï¼å1ï¼å2ï¼9å3ï¼7å5ï¼6å6é½æè¿ä¸ªç¹æ§ãå ±åçç¹ç¹æ¯ä¸¤è ç¸å çäºæ¨¡ã
对äºè®¡ç®æºï¼å ¶æ¦å¿µåæ¹æ³å®å ¨ä¸æ ·ãnä½è®¡ç®æºï¼è®¾n=8ï¼ æè½è¡¨ç¤ºçæ大æ°æ¯ï¼è¥åå 1æ为(9ä½ï¼ï¼ä½å åªæ8ä½ï¼æé«ä½1èªç¶ä¸¢å¤±ãååäºï¼æ以8ä½äºè¿å¶ç³»ç»ç模为2^8ãå¨è¿æ ·çç³»ç»ä¸åæ³é®é¢ä¹å¯ä»¥åæå æ³é®é¢ï¼åªéæåæ°ç¨ç¸åºçè¡¥æ°è¡¨ç¤ºå°±å¯ä»¥äºãæè¡¥æ°ç¨å°è®¡ç®æºå¯¹æ°çå¤çä¸ï¼å°±æ¯è¡¥ç ã
åèèµæï¼
è¡¥ç âç¾åº¦ç¾ç§
计算机中的原代码、补码、源码逆码怎么表示?
一、源码小数部分的源码上海溯源码燕窝品牌怎么样原码和补码可以表示为两个复数的分子和分母,然后计算二进制小数系统,源码根据下面三步的源码方法就会找出小数源代码和补码的百位形式。/=B/2^6=0.B
-/=B/2^7=0.B
二、源码将十进制十进制原始码和补码转换成二进制十进制,源码然后根据下面三步的源码方法求出十进制源代码和补码形式。一个
0.=0.B
0.=0.B
三、源码二进制十进制对应的源码原码和补码
[/]源代码=[0.B]源代码=B
[-/]源代码=[0.b]源代码=B
[0.]原码=[0.b]原码=B
[0.]源代码=[0.B]源代码=B
[/]补体=[0.B]补体=B
[-/]补体=[0.b]补体=B
[0.]补码=[0.b]补码=B
[0.]补体=[0.B]补体=B
扩展资料:
原码、逆码、源码补码的源码dubbo底层源码教程使用:
在计算机中对数字编码有三种方法,对于正数,这三种方法返回的结果是相同的。
+1=[原码]=[逆码]=[补码]
对于这个负数:
对计算机来说,加、减、乘、除是python乘法口诀源码最基本的运算。有必要使设计尽可能简单。如果计算机能够区分符号位,那么计算机的基本电路设计就会变得更加复杂。
负的正数等于正的负数,2-1等于2+(-1)所以这个机器只做加法,不做减法。符号位参与运算,cdhd源码混合指标只保留加法运算。
(1)原始代码操作:
十进制操作:1-1=0。
1-1=1+(-1)=[源代码]+[源代码]=[源代码]=-2。
如果用原代码来表示,让符号位也参与计算,对于减法,结果显然是蜜獾源码分析不正确的,所以计算机不使用原代码来表示一个数字。
(2)逆码运算:
为了解决原码相减的问题,引入了逆码。
十进制操作:1-1=0。
1-1=1+(-1)=[源代码]+[源代码]=[源代码]+[源代码]=[源代码]=[源代码]=-0。
使用反减法,结果的真值部分是正确的,但在特定的值“0”。虽然+0和-0在某种意义上是相同的,但是0加上符号是没有意义的,[源代码]和[源代码]都代表0。
(3)补充操作:
补语的出现解决了零和两个码的符号问题。
十进制运算:1-1=0。
1-1=1+(-1)=[原码]+[原码]=[补码]+[补码]=[补码]=[原码]=0。
这样,0表示为[],而之前的-0问题不存在,可以表示为[]-。
(-1)+(-)=[源代码]+[源代码]=[补充]+[补充]=[补充]=-。
-1-的结果应该是-。在补码操作的结果中,[补码]是-,但是请注意,由于-0的补码实际上是用来表示-的,所以-没有原码和逆码。(-的补码表[补码]计算出的[原码]是不正确的)。


