1.求python支持向量机多元回归预测代码
2.求python支持向量机数据设置标签代码
3.机器学习算法之——支持向量机(Support Vector Machine）讲解及Python实现
4.一文带您了解支持向量机算法(SVM:Support Vector Machine):Python示例
5.机器学习系列1-支持向量机(SVM)
6.算法篇|23SVM（下）：如何进行乳腺癌检测？

求python支持向量机多元回归预测代码

       这是一段用 Python 来实现 SVM 多元回归预测的代码示例：

       # 导入相关库

       from sklearn import datasets

       from sklearn.svm import SVR

       from sklearn.model_selection import train_test_split

       from sklearn.metrics import mean_squared_error

       # 加载数据集

       X, y = datasets.load_boston(return_X_y=True)

       # 将数据集拆分为训练集和测试集

       X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

       # 创建SVM多元回归模型

       reg = SVR(C=1.0, epsilon=0.2)

       # 训练模型

       reg.fit(X_train, y_train)

       # 预测结果

       y_pred = reg.predict(X_test)

       # 计算均方误差

       mse = mean_squared_error(y_test, y_pred)

       print("Mean Squared Error:", mse)

       在这段代码中，首先导入了相关的库，包括 SVR 函数、train_test_split 函数和 mean_squared_error 函数。然后，使用 load_boston 函数加载数据集，maven 打包 打上源码并将数据集分为训练集和测试集。接着，使用 SVR 函数创建了一个 SVM 多元回归模型，并使用 fit 函数对模型进行训练。最后，使用 predict 函数进行预测，并使用 mean_squared_error 函数计算均方误差。

       需要注意的是，这仅仅是一个示例代码，在实际应用中，可能需要根据项目的需求进行更改，例如使用不同的超参数

求python支持向量机数据设置标签代码

       以下是使用Python中的Scikit-learn库实现支持向量机（SVM）模型的数据设置标签代码示例：

       from sklearn import svm

       # 假设有以下三个样本的数据：

       X = [[0, 0], [1, 1], [2, 2]]

       y = [0, 1, 1]  # 对应每个数据点的标签，0表示负样本，1表示正样本

       # 创建SVM模型

       clf = svm.SVC()

       # 将数据集(X)和标签(y)作为训练数据来训练模型

       clf.fit(X, y)

       上述代码中，X是php两个源码合并一个二维数组，每个元素都代表一个数据点的特征值，y是一个一维数组，每个元素都代表对应数据点的标签。通过将X和y作为训练数据，可以训练SVM模型并得到分类结果。

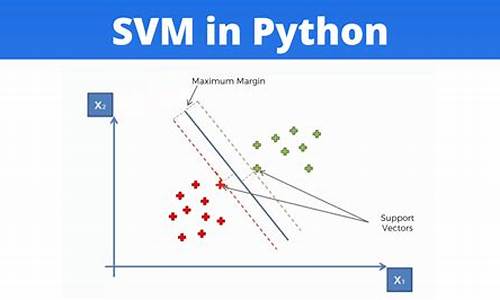
机器学习算法之——支持向量机(Support Vector Machine）讲解及Python实现

       从本周开始，我们将深入探讨机器学习竞赛中的基础且广泛应用的算法——支持向量机(Support Vector Machine, SVM)。即使不是为了比赛的名次，理解这些基本模型也是必不可少的。今天，我们将从SVM的基本概念讲起。

       SVM是一种经典的二分类模型，属于监督学习方法。其核心思想是找到一个最优的超平面，该超平面能够最大化样本间的间隔，形成一个凸二次规划问题。当样本线性可分时，SVM的目标是找到一条能将正负样本分开，且对扰动最不敏感的直线，即所谓的合成团圆饭源码“支持向量”所决定的超平面。

       区分线性可分和非线性可分的关键在于，线性可分是指用直线（在低维空间）或平面（高维空间）就能清晰划分两类样本，而非线性可分则需要更复杂的模型。对于非线性问题，通过核函数，我们可以将样本映射到更高维空间，使得线性分类变得可能。

       SVM的学习过程涉及拉格朗日乘子法和KKT条件，这是一种求解有约束优化问题的有效方法。通过引入松弛变量，线性不可分问题得到了缓解，形成了软间隔支持向量机，它允许一些样本点稍微偏离间隔边界。

       在实际应用中，SVM有其独特优势，如高分类精度、对少量数据的处理能力强和解决非线性问题的能力。然而，它也存在挑战，如在大量数据和多参数选择上的通达信全军出击源码计算复杂性，以及对缺失数据的敏感性。

       现在，你可以通过这个链接测试自己对SVM的理解：[链接]。进一步学习其他机器学习算法，如HMM、决策树、梯度提升和逻辑回归，可以在这里找到：[延伸阅读]。

一文带您了解支持向量机算法(SVM:Support Vector Machine):Python示例

       SVM，即支持向量机，是一种用于分类和回归任务的机器学习算法。其核心目标是找到一个最优超平面，使得不同类别的数据点在N维空间中清晰分开，并最大化超平面与数据点之间的间隔。超平面是将数据点进行分割的决策边界，支持向量是那些最接近超平面并影响其位置和方向的数据点。

       SVM在机器学习中广泛应用，如图像分类、文本分类、生物信息学和金融领域等。八子燕窝饮品溯源码它具有出色的泛化能力和鲁棒性，但需仔细选择核函数和调整超参数以获得最佳性能。

       超平面是一维线性边界，二维平面边界，或更高维度的空间分割面。支持向量决定了超平面的位置和分类边界。通过找到具有最大间隔的超平面，SVM提高分类器性能和鲁棒性，应对新的、未曾见过的数据点。

       核函数的出现是为了在原始数据难以线性分割的情况下，通过将数据映射到高维特征空间，在高维空间中找到超平面进行有效分割。核函数通过数学技巧将数据转换到更高维度空间，使用线性分析方法处理复杂非线性数据分布。核函数包括线性核、多项式核、RBF核、Sigmoid核和高斯核等。

       下面以鸢尾花数据集为例，演示不同核函数在SVM分类中的效果。首先导入必要库并加载数据集，然后使用线性核、Sigmoid核、RBF核、多项式核进行SVM分类示例。核函数的选择取决于问题和数据集，线性核适用于线性可分数据，高斯核适合复杂数据分布，多项式核在数据归一化后表现良好。正确选择核函数可提高分类性能。

       支持向量机算法提供了一种优雅而强大的解决分类问题的方法。

机器学习系列1-支持向量机(SVM)

       开始介绍机器学习系列的首个内容，我们将使用sklearn自带的鸢尾花数据集进行支持向量机(SVM)的实战演示。

       SVM是一种强大的监督学习工具，其核心目标是在高维空间中寻找一个最优的决策边界，最大化不同类别数据点的间隔，以实现高效分类和回归任务。

       首先，了解鸢尾花数据集：这是一个包含个样本的三分类问题，每个样本有四个特征，代表三种不同品种的鸢尾花。我们将随机选取%的数据作为测试集，其余用于训练。

       创建SVM分类器时，其背后的数学原理涉及找到一个超平面，使得所有数据点到该面的间隔最大化。具体来说，我们需确保正确分类训练点，并通过优化问题找到最优解。利用拉格朗日乘子法，我们将原始问题转化为最优化形式，通过Python代码实现，如使用线性核(kernel='linear')，C=1.0的正则化。

       接下来，我们将运用这些理论知识，通过代码预测鸢尾花品种，并计算预测的准确率，展示SVM在实际问题中的应用效果。

算法篇|SVM（下）：如何进行乳腺癌检测？

       在 Python 的 sklearn 工具包中有 SVM 算法，首先需要引用工具包： from sklearn import svm。SVM 可以用于分类和回归。当做分类器时，使用 SVC 或者 LinearSVC。SVC 是用于处理非线性数据的分类器，可以使用线性核函数或高维核函数进行划分。

       创建一个 SVM 分类器的步骤如下：model = svm.SVC(kernel='rbf', C=1.0, gamma='auto')。参数 kernel 用于选择核函数，C 控制目标函数的惩罚系数，gamma 是核函数的系数。

       训练 SVM 分类器时，使用 model.fit(train_X,train_y)，其中 train_X 是特征值矩阵，train_y 是分类标识。预测时，使用 model.predict(test_X)，其中 test_X 是测试集中的样本特征矩阵。

       创建线性 SVM 分类器，使用 model=svm.LinearSVC()。LinearSVC 适用于线性分类问题，且效率更高。

       乳腺癌检测实际项目使用 SVM 分类器，数据集来自美国威斯康星州的乳腺癌诊断数据集。数据集包含个字段，特征值有平均值、标准差、最大值。通过清洗数据、筛选特征、进行相关性分析等步骤，选择关键特征进行分类。

       具体步骤包括：加载数据、清洗数据、特征筛选和相关性分析，使用热力图进行可视化。最终选择6个关键特征进行训练和预测，准确率超过%。

       使用 sklearn 提供的 SVM 工具，简化了创建和训练的过程。实践项目中，需要熟练掌握每个流程，提高数据敏感度和数据化思维能力。

       思考题：使用 LinearSVC 和全部特征（除 ID 外）进行乳腺癌分类，评估准确度；分享对 sklearn 中 SVM 使用的体会。

       学习笔记总结了使用 sklearn 实现 SVM 分类的流程，并通过实际项目展示了乳腺癌检测的应用。强烈推荐学习《数据分析实战 讲》课程，深入掌握数据分析实战技能。

求python多元支持向量机多元回归模型最后预测结果导出代码、测试集与真实值R2以及对比图代码

       这是一个多元支持向量机回归的模型，以下是一个参考的实现代码：

       import numpy as npimport matplotlib.pyplot as pltfrom sklearn import svmfrom sklearn.metrics import r2_score

       # 模拟数据

       np.random.seed(0)

       X = np.sort(5 * np.random.rand(, 1), axis=0)

       y = np.sin(X).ravel()

       y[::5] += 3 * (0.5 - np.random.rand())

       # 分割数据

       train_X = X[:]

       train_y = y[:]

       test_X = X[:]

       test_y = y[:]

       # 模型训练

       model = svm.SVR(kernel='rbf', C=1e3, gamma=0.1)

       model.fit(train_X, train_y)

       # 预测结果

       pred_y = model.predict(test_X)# 计算R2r2 = r2_score(test_y, pred_y)

       # 对比图

       plt.scatter(test_X, test_y, color='darkorange', label='data')

       plt.plot(test_X, pred_y, color='navy', lw=2, label='SVR model')

       plt.title('R2={ :.2f}'.format(r2))

       plt.legend()

       plt.show()

       上面的代码将数据分为训练数据和测试数据，使用SVR模型对训练数据进行训练，然后对测试数据进行预测。计算预测结果与真实值的R2，最后将结果画出对比图，以评估模型的效果。