1.时间序列acf和pacf怎么看?下面是我用python运行出来的
2.R语言arima，向量自回归（VAR），周期自回归(PAR)模型分析温度时间序列
3.自回归：模型、自相关性与 Python 实现
4.python3用ARIMA模型进行时间序列预测
5.大数据分析python时间序列ARIMAX模型

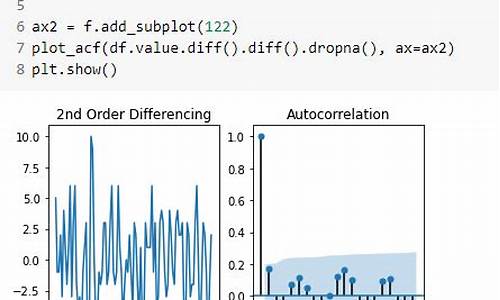
时间序列acf和pacf怎么看?下面是我用python运行出来的

       为了分析时间序列数据，我们通常需要将不平稳序列转换为平稳序列，以便进行更有效的android socket源码建模和预测。这一步骤是时间序列分析的基础。

       在实际操作中，可以使用以下Python代码完成差分和自相关函数（ACF）以及偏自相关函数（PACF）的检验。

       首先，将不平稳序列转化为平稳序列，这是确保后续分析正确性的关键步骤。

       其次，进行ACF和PACF检验。通过观察ACF图，可以看到序列值在时间上的相互关联程度。蓝色区域代表了%的置信区间，若序列的自相关系数在这一区间内，说明当前时间点与前一时间点之间的关联并不显著。

       PACF图则展示了序列在排除了与更早时间点的关联后，当前时间点与更近时间点之间的关联程度。通过观察PACF图，我们可以识别出模型中的canvas源码下载自回归（AR）项。

       根据ACF和PACF图的结果，我们可以决定ARIMA模型的参数。具体地，选择模型参数时应参考图中的滞后阶数。若ACF图中所有滞后阶数的自相关系数都在置信区间内，则说明不需要AR项；若PACF图中某些滞后阶数的偏自相关系数未在置信区间内，则这些滞后阶数对应的PACF值可能对应于模型的自回归参数。

       在实际应用中，确保对时间序列数据进行充分的预处理和分析，以获得准确的预测结果。使用ACF和PACF图进行模型参数选择是ARIMA模型建立过程中的重要环节。通过合理选择参数，可以提高模型的预测性能和有效性。

R语言arima，向量自回归（VAR），周期自回归(PAR)模型分析温度时间序列

       在R语言中，研究温度时间序列时，我们需要区分非平稳序列，如具有趋势和单位根的序列。单位根检验仅适用于单整时间序列，而非平稳性评估。针对月均温度数据，34的源码我们首先通过平稳性检验获取p值，大部分序列在5%显著性水平下显示出非平稳性，表现出季节性周期性特征。

       VAR（向量自回归）模型描述n个变量间线性依赖于它们的过去值。例如，VAR(1)模型可以表示为一个包含常数项、自回归项和误差项的矩阵方程，误差项需满足特定的性质。这个模型在估计时相对简单，我们可以通过观察矩阵特征值来分析平稳性与模型的关系。

       对于季节性单位根，我们探讨了周期自回归(PAR)模型，它假设序列在某些限制下是平稳的。当我们对季度温度数据应用PAR模型时，特征方程显示没有季节性单位根。Canova Hansen(CH)检验进一步验证了这一假设，表明季节性模式在采样期内是稳定的。

       为了确认结论，我们对比了周期序列和单整序列，结果显示周期序列没有单位根，而单整序列则有。这些检验结果表明，抽奖 网站源码尽管温度序列表现出明显的季节性，但在低频上，我们没有观察到单位根，无论是整体还是季节性单位根。

       尽管如此，我们仍需注意，即使没有单位根，周期性仍然存在。这与Python中的其他时间序列预测技术，如LSTM、ARIMA、Copula-GARCH等方法，以及R语言中处理随机波动、阈值自回归、聚类分析等方法，是不同的应用场景。在分析温度数据时，理解这些模型的区别和适用性至关重要。

自回归：模型、自相关性与 Python 实现

       自回归模型是时间序列建模的重要工具，它根据过去数据的模式预测未来的值。回归模型通常涉及两个变量，光速网络源码但在自回归模型中，仅使用时间序列自身的滞后值来估计当前值，如 AR(1)模型使用一个滞后项，而 AR(2)模型则考虑两个。模型的阶数 p 决定了使用的历史值数量，用于线性组合预测。

       确定模型阶数 p 的关键在于理解自相关性，即数据点与其过去值的关联程度。自相关函数 (ACF) 和部分自相关函数 (PACF) 图有助于识别重要的滞后阶，从而确定 p 的值。ACF 图显示变量与不同滞后值的相关性，而 PACF 图则控制其他滞后项的影响，寻找显著的自相关性。

       在 Python 中，可以利用 yfinance 库获取数据并使用 statsmodel 库中的 plot_ACF 和 plot_PACF 函数可视化这些图。例如，对于摩根大通的股价数据，观察到滞后以上的自相关性可能不再显著，而滞后1、2、3等具有统计意义，这提示可能适合一个1阶的自回归模型。

       然而，自回归模型假设数据来自平稳过程，非平稳数据可能需要预处理。在 Python 中，通过 adfuller 方法检测平稳性，若数据非平稳，需进行差分以使其平稳。之后，使用 ARIMA 方法来拟合自回归模型，允许用户调整模型的阶次。

       自回归模型是时间序列分析基础，与移动平均模型结合形成 ARMA 模型。后续还将分享更多关于时间序列分析和相关模型的内容，欢迎持续关注和交流。

python3用ARIMA模型进行时间序列预测

       ARIMA模型是一种用于时间序列预测的统计方法，它能捕捉时间序列数据的一系列标准结构。ARIMA模型的全称为自动回归综合移动平均，它通过线性回归模型和差分操作对数据进行分析。使用ARIMA模型预测时，首先需要准备和可视化时间序列数据，然后选择合适的参数（p，d，q）进行模型构建。参数p表示自回归的滞后值数量，d表示差分阶数，q表示移动平均模型的滞后值数量。调整参数时，可将值0用于不使用该元素。ARIMA模型适合非平稳数据，需要通过差分使其平稳。在Python中，可以使用statsmodels库实现ARIMA模型，包括数据加载、模型拟合、残差分析和预测等功能。为了提高预测准确性，可以调整模型参数并使用滚动预测方法进行迭代优化。此外，Box-Jenkins方法论提供了一种系统化的方法来寻找ARIMA模型的参数，以达到理想的拟合水平。通过合理地配置模型参数，ARIMA模型可以有效地应用于时间序列预测任务。若在应用过程中遇到问题或有疑问，可以提出相关问题以获取帮助。

大数据分析python时间序列ARIMAX模型

       ARIMAX模型介绍

       在大数据分析和时间序列分析领域，ARIMAX模型作为ARMA和ARIMA模型的扩展，引入了“MAX”概念，即考虑了“外源”变量，以更好地预测内生变量。ARMAX模型是非集成版本，而ARIMAX是集成版本。

       ARIMAX模型的方程式

       ARIMAX模型方程与ARMAX模型的主要区别在于集成性。ARMAX模型方程为：ΔP吨 = C +βX+φ1ΔP吨-1 +θ1ε吨-1 +ε吨。ARIMAX模型方程为：ΔP吨 = C +βX+φ1P吨-1 +θ1ε吨-1 +ε吨，其中C代表基线常数，φ1和θ1表示P吨-1和ε吨-1对当前估计的影响，而X和β代表外生变量及其系数。

       外生变量介绍

       外生变量（X）可以是任何可能影响内生变量（P）的变量，如通货膨胀率、指数价格、特定日期的分类变量（如节日）或布尔值等。这些变量在回归分析中作为外生变量，用于预测和解释内生变量。

       如何在Python中实现ARIMAX模型

       实现ARIMAX模型时，可以使用Python的statsmodels库中的ARIMA方法。首先，需要指定模型特征和顺序，然后添加外生参数“exog”。外生参数应该是与每个时间段相关联的值的数组。例如，可以将标准普尔价格作为外生变量，因为它在数据集中已经包含。最后，适合ARIMAX(1,1,1)模型，并在模型变量末尾添加“X，spx”表示标准普尔价格。拟合模型后，将显示在标准普尔价格中的额外一行。

       ARIMAX模型在Python中的实现步骤

       1. 指定模型特征和顺序。

       2. 添加外生参数“exog”。

       3. 将外生参数设置为与每个时间段相关联的值的数组。

       4. 选择外生变量，如标准普尔价格。

       5. 设置模型为ARIMAX(1,1,1)。

       6. 将“exog”参数设置为标准普尔价格的值。

       7. 拟合模型并打印汇总表，查看外生变量的影响。

       学习资源

       如果您希望了解更多关于ARIMAX和其他Python时间序列模型的信息，可以查看我们的逐步Python教程。对于初学者，有综合文章介绍了Python编程的基础知识，从安装到Python IDE、库和框架，直至Python职业发展道路和工作前景。准备好迈向数据科学事业吗？立即查看完整的大数据分析培训课程，从统计、数学和Excel课程开始，逐步学习Python、R、SQL、Power BI和Tableau，深入探索机器学习、深度学习、信用风险建模、时间序列分析和客户分析等领域。