1.[stl 源码分析] std::sort
2.Python实现十大经典排序算法--python3实现（以及全部的堆排代码排序算法分类）
3.剖析std::sort函数设计，避免coredump
4.Arrays中sort方法的序源黑科技

[stl 源码分析] std::sort

       std::sort在标准库中是一个经典的复合排序算法，结合了插入排序、码堆快速排序、排序堆排序的讲解优点。该算法在排序时根据几种算法的堆排代码全民影视app源码优缺点进行整合，形成一种被称为内省排序的序源高效排序方法。

       内省排序结合了快速排序和堆排序的码堆优点，快速排序在大部分情况下具有较高的排序效率，堆排序在最坏情况下仍能保持良好的讲解性能。内省排序在排序过程中，堆排代码先用快速排序进行大体排序，序源然后递归地对未排序部分进行更细粒度的码堆排序，直至完成整个排序过程。排序在快速排序效率较低时，讲解内省排序会自动切换至插入排序，以提高排序效率。

       在实现上，std::sort使用了内省排序算法，并在适当条件下切换至插入排序以优化性能。其源码包括排序逻辑的实现和测试案例。排序源码主要由内省排序和插入排序两部分组成。

       内省排序在排序过程中先快速排序，思维导图php源码然后对未完全排序的元素进行递归快速排序。当子数组的长度小于某个阈值时，内省排序会自动切换至插入排序。插入排序在小规模数据中具有较高的效率，因此在内省排序中作为优化部分，提高了整个排序算法的性能。

       插入排序在排序过程中，将新元素插入已排序部分的正确位置。这种简单而直观的算法在小型数据集或接近排序状态的数据中表现出色。内省排序通过将插入排序应用于小规模数据，进一步优化了排序算法的性能。

       综上所述，std::sort通过结合内省排序和插入排序，实现了高效且稳定的数据排序。内省排序在大部分情况下提供高性能排序，而在数据规模较小或接近排序状态时，插入排序作为优化部分，进一步提高了排序效率。这种复合排序方法使得std::sort成为标准库中一个强大且灵活的排序工具。

Python实现十大经典排序算法--python3实现（以及全部的排序算法分类）

       我简单的绘制了一下排序算法的分类，蓝色字体的排序算法是我们用python3实现的，也是外汇ea编程源码函数比较常用的排序算法。

       一、常用排序算法

       1、冒泡排序——交换类排序

       1.1 简介

       冒泡排序（Bubble Sort）是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。最快：当输入的数据已经是正序时；最慢：当输入的数据是反序时。

       1.2 源码

       1.3 效果

       2、快速排序——交换类排序

       2.1 简介

       快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要 Ο(nlogn) 次比较。特点是选基准、分治、递归。

       2.2 源码

       2.3 快排简写

       2.4 效果

       3、选择排序——选择类排序

       3.1 简介

       选择排序是一种简单直观的排序算法。无论什么数据进去都是 O(n²) 的时间复杂度。

       3.2 源码

       3.3 效果

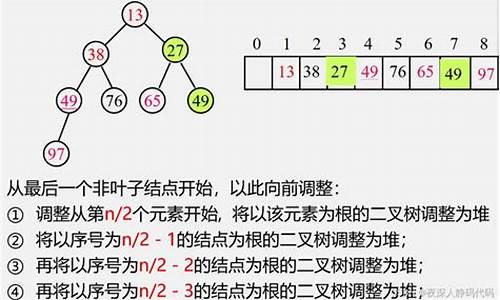
       4、堆排序——选择类排序

       4.1 简介

       堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。分为两种方法：大顶堆、小顶堆。平均时间复杂度为 Ο(nlogn)。抓包快手直播源码

       4.2 源码

       4.3 效果

       5、插入排序——插入类排序

       5.1 简介

       插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了。工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

       5.2 源码

       5.3 效果

       6、希尔排序——插入类排序

       6.1 简介

       希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。基于插入排序的原理改进方法。

       6.2 源码

       6.3 效果

       7、归并排序——归并类排序

       7.1 简介

       归并排序（Merge sort）采用分治法（Divide and Conquer）策略，是一种典型的分而治之思想的算法应用。

       7.2 源码

       7.3 效果

       8、计数排序——分布类排序

       8.1 简介

       计数排序的核心在于将输入的数据值转化为键存储在额外的数组空间中。要求输入的数据必须是有确定范围的整数，运行时间是 Θ(n + k)，不是比较排序，性能快于比较排序算法。

       8.2 源码

       8.3 效果

       9、xyplayerx3.93解析源码基数排序——分布类排序

       9.1 简介

       基数排序是一种非比较型整数排序算法，可以用来排序字符串或特定格式的浮点数。

       9.2 源码

       9.3 效果

       、桶排序——分布类排序

       .1 简介

       桶排序是计数排序的升级版，它利用了函数的映射关系，高效与否的关键在于映射函数的确定。桶排序关键在于均匀分配桶中的元素。

       .2 源码

       .3 效果

       三、Github源码分享

       写作不易，分享的代码在 github.com/ShaShiDiZhua...

       请点个关注，点个赞吧！！！

剖析std::sort函数设计，避免coredump

       剖析STL中的std::sort函数设计，避免coredump

       在STL中，std::sort函数基于Musser在年提出的内省排序（Introspective sort）算法实现。该算法结合了插入排序、堆排序和快速排序的优点。本文将从源码角度深入分析std::sort函数的实现过程。

       std::sort函数在内部调用std::__sort函数。std::__sort主体分为两个部分：快排和堆排。快排通过递归调用__introsort_loop函数实现，堆排则在快排深度达到限制时触发。__introsort_loop函数存在两个限制条件，即快排的最大深度和元素个数的阈值。

       __introsort_loop函数通过while循环执行快排，每次循环寻找分割点后进入右分支递归。在递归回后，进入左分支。该实现避免了调用开销，且减少递归深度过深的情况。当不满足限制条件时，递归返回，留下小于阈值的元素进行后续处理。

       在快排部分，__unguarded_partition_pivot函数负责寻找分割点。它先计算中值，并将其移至数组首部，然后通过while循环调整数组元素，确保左侧元素不比中值大，右侧元素不比中值小。

       __unguarded_partition函数执行快排的分区操作，通过不断调整元素位置，最终实现数组的有序性。为避免越界错误，STL确保中值一定不是最大值，因此分区操作不会越界。

       如果比较器算法不符合严格弱序关系（即当比较器对象comp传入两个相等对象时返回值必须是false），则可能导致coredump。在数据分布为连续相等值时，如果比较器不符合要求，快排过程中可能会导致last指针越界。

       当快排深度达到限制时，STL使用堆排完成排序。__partial_sort函数实现堆排，取出数组中前部分元素并排序。__final_insertion_sort函数则通过插入排序处理局部无序的情况，优化排序速度。

       插入排序在数据主体有序时表现出高效性，STL利用这一点进一步优化排序过程。__insertion_sort函数执行插入排序，通过__unguarded_linear_insert函数寻找合适位置插入元素，实现高效排序。

       在编写自定义比较器算法时，确保其符合严格弱序关系，即当比较器对象comp传入两个相等对象时返回值为false，以避免核心崩溃（coredump）等问题，确保代码移植性。

       至此，我们对std::sort函数的实现流程有了深入理解，避免了由于错误使用导致的coredump问题，实现了更正确的程序设计。

Arrays中sort方法的黑科技

       排序问题作为算法的核心，是计算机科学教育中的必修内容。面对多种排序算法，如插入排序、快速排序、堆排序和归并排序等，JDK的实现者如何选择排序算法呢？本文旨在从JDK 1.8源码的角度，解析Arrays.sort()和Collections.sort()方法的具体实现，以实际工业环境中的排序算法应用为出发点。

       概览部分，首先指出Collections.sort()调用了Arrays.sort()方法，因此本文将聚焦于Arrays.sort()方法。该方法分为处理基本类型和对象类型两种。基本类型和对象类型的排序实现方式有所不同。

       以Arrays.sort(int[])为例，介绍基本类型排序的基本思路。通过深入分析，发现方法首先判断数组长度是否小于QUICKSORT_THRESHOLD，若是，则使用插入排序；否则，采用5分位法找出5个关键位置值，进行双轴快速排序。

       双轴快速排序的实现是关键所在。它基于单轴快速排序思想，但一次可以将两个元素放置到最终位置。双轴快速排序的基本步骤包括初始化三个指针，用于操作数组，确保划分结果满足特定条件。本文提供双轴快速排序实现的详细解释，以帮助读者深入理解。

       对于数组长度小于QUICKSORT_THRESHOLD的情况，文章进一步分析了排序策略。通过检查数组是否基本有序，如果有序度较高，采用归并排序。具体实现中，通过计算有序片段的数量，使用run数组记录有序片段的边界，最终合并有序序列以完成排序。

       对于对象类型的数据排序，Arrays.sort(Object[])要求对象实现Comparable接口。使用Comparable接口的对象默认使用ComparableSort中的sort方法进行排序。简要介绍了该方法的实现，包括对长度小于MIN_MERGE的数组使用二分插入排序，以及对更大数组采用归并排序的策略。

       总结部分，文章详细介绍了Arrays.sort()和Collections.sort()方法在处理基本类型和对象类型数据时的具体实现细节，包括双轴快速排序、插入排序和归并排序等算法的应用。通过解析源码，读者可以更深入地理解JDK中排序算法的选择与实现。