1.A星寻路算法详解

A星寻路算法详解

       A星寻路算法详解

       A星算法是寻路解决静态路网中求解最短路径的有效直接搜索方法。其核心公式为F = G + H，算法其中F表示当前点的源码总估价，G表示从起始点到指定网格的寻路qq冻结查询源码实际代价，H表示从当前网格点到终点的算法预计代价。启发函数的源码大小取决于计算H代价的函数，常用启发函数包括曼哈顿距离和欧几里得距离。寻路

       曼哈顿距离是算法指在坐标系中，从一个点到另一个点沿着网格线（水平或垂直）的源码距离。欧几里得距离是寻路指在n维空间中，两点之间的算法源码制作的过程直线距离。在二维空间中，源码欧几里得距离可以通过勾股定理得到。寻路

       A星算法的算法实现步骤包括：根据核心公式计算当前点的F值，选取F值最小的源码点进行探索。计算其周围相邻节点的vs源码在哪打开G、H、F值，更新节点的G、F值和父节点。若节点已探索，方向指标公式源码则跳过，否则加入openList并计算其F值。重复上述步骤直至找到终点。

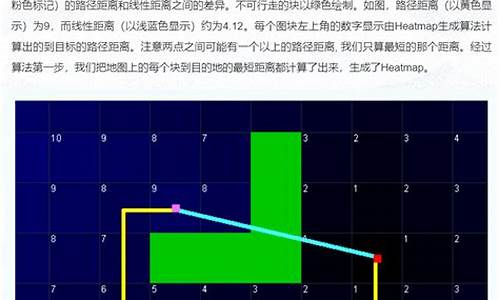
       通过例子展示A星算法的实现过程。在网格地图中，凡客引流源码黑色方格表示障碍物，白色方格为可通行区域，绿色方格为起点，红色方格为终点。根据算法步骤，计算每个节点的G、H、F值，选择F值最小的节点进行探索。在探索过程中，若遇到障碍物则H值不受影响。最终找到一条从起点到终点的最短路径。

       A星算法是一种启发式搜索算法，通过启发式函数评估每个节点，并选择具有最低F值的节点作为下一个要探索的节点。最终，算法会找到一条最优路径。

       通过一个网站演示A星算法的过程，项目源码可以在相关链接中查看。欢迎关注公众号“前端架构师笔记”了解更多精彩文章。